.

In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and (1 − r), all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in propositions four through eight of his Book of Lemmas. Arbelos literally means "shoemaker's knife" in Greek; it resembles the blade of a knife used by ancient cobblers.[1]

Properties

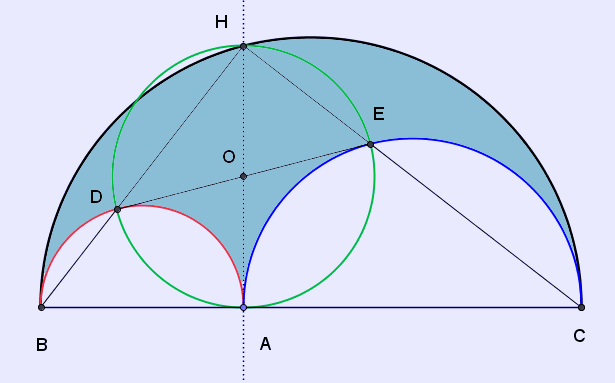
Arbelos diagram with points marked

Area

A circle with a diameter HA is equal in area with the arbelos
Proof

If BC = 1 and BA = r, then

In triangle BHA: \( r^2+h^2=x^2 \)
In triangle CHA: \( (1-r)^2+h^2=y^2 \)
In triangle BHC: \( x^2+y^2=1 \)

By substitution: \( y^2=(1-r)^2+x^2-r^2 \). By expansion: \( y^2=1-2r+x^2 \(. By substituting for y2 into the equation for triangle BHC and solving for x:

\( x=\sqrt{r} \)

By substituting this, solve for y and h

\( y=\sqrt{1-r} \)
\( h=\sqrt{r-r^2} \)

The radius of the circle with center O is:

\( \frac{1}{2}\sqrt{r-r^2}. \)

Therefore, the area is:

\( A_{circle}=\pi\left(\frac{1}{2}\sqrt{r-r^2}\right)^2 \)
\( A_{circle}=\frac{\pi r}{4}-\frac{\pi r^2}{4} \)

The area of the arbelos is the area of the large semicircle minus the area of the two smaller semicircles. Therefore the area of the arbelos is:

\( A_{arbelos}=\frac{\pi}{8}-\left(\frac{\pi}{2}\left(\frac{r}{2}\right)^2+\frac{\pi}{2}\left(\frac{1-r}{2}\right)^2\right) \)
\( A_{arbelos}=\frac{\pi-\pi r^2-\pi+2\pi r-\pi r^2}{8} \)
\( A_{arbelos}=\frac{\pi r}{4}-\frac{\pi r^2}{4}=A_{circle} \)

Q.E.D.[2]

This property appears as Proposition 4 in Archimedes' Book of Lemmas:

If AB be the diameter of a semicircle and N any point on AB, and if semicircles be described within the first semicircle and having AN, BN as diameters respectively, the figure included between the circumferences of the three semicircles is [what Archimedes called "αρβελοσ"]; and its area is equal to the circle on PN as diameter, where PN is perpendicular to AB and meets the original semicircle in P.

[3]
Rectangle

The segment BH intersects the semicircle BA at D. The segment CH intersects the semicircle AC at E. Then DHEA is a rectangle.

Proof: Angles BDA, BHC, and AEC are right angles because they are inscribed in semicircles (by Thales' theorem). The quadrilateral ADHE therefore has three right angles, so it is a rectangle. Q.E.D.

Tangents

The line DE is tangent to semicircle BA at D and semicircle AC at E.

Proof: Since angle BDA is a right angle, angle DBA equals π/2 minus angle DAB. However, angle DAH also equals π/2 minus angle DAB (since angle HAB is a right angle). Therefore triangles DBA and DAH are similar. Therefore angle DIA equals angle DOH, where I is the midpoint of BA and O is the midpoint of AH. But AOH is a straight line, so angle DOH and DOA are supplementary angles. Therefore the sum of angles DIA and DOA is π. Angle IAO is a right angle. The sum of the angles in any quadrilateral is 2π, so in quadrilateral IDOA, angle IDO must be a right angle. But ADHE is a rectangle, so the midpoint O of AH (the rectangle's diagonal) is also the midpoint of DE (the rectangle's other diagonal). As I (defined as the midpoint of BA) is the center of semicircle BA, and angle IDE is a right angle, then DE is tangent to semicircle BA at D. By analogous reasoning DE is tangent to semicircle AC at E. Q.E.D.