.

In mathematics, a complex torus is a particular kind of complex manifold M whose underlying smooth manifold is a torus in the usual sense (i.e. the cartesian product of some number N circles). Here N must be the even number 2n, where n is the complex dimension of M.

All such complex structures can be obtained as follows: take a lattice Λ in Cⁿ considered as real vector space; then the quotient group

Cⁿ/Λ

is a compact complex manifold. All complex tori, up to isomorphism, are obtained in this way. For n = 1 this is the classical period lattice construction of elliptic curves. For n > 1 Bernhard Riemann found necessary and sufficient conditions for a complex torus to be an algebraic variety; those that are varieties can be embedded into complex projective space, and are the abelian varieties.

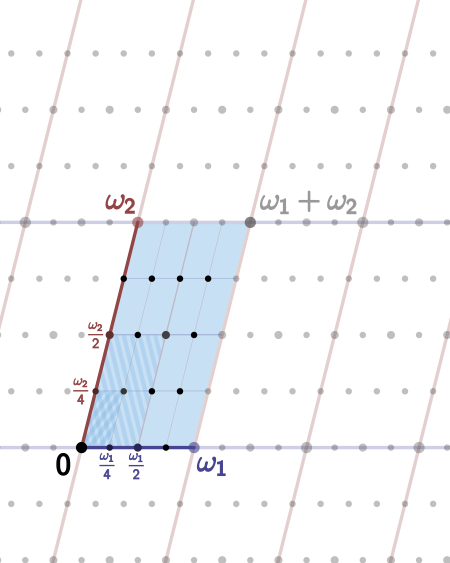
The complex torus associated to a lattice spanned by two periods, ω₁ and ω₂. Corresponding edges are identified.

The actual projective embeddings are complicated (see equations defining abelian varieties) when n > 1, and are really coextensive with the theory of theta-functions of several complex variables (with fixed modulus). There is nothing as simple as the cubic curve description for n = 1. Computer algebra can handle cases for small n reasonably well. By Chow's theorem, no complex torus other than the abelian varieties can 'fit' into projective space.

.

Complex torus