.
Eckmann–Hilton duality
In the mathematical disciplines of algebraic topology and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram for a particular concept and reversing the direction of all arrows, much as in category theory with the idea of the opposite category.
It is named after Beno Eckmann and Peter Hilton.
For example, the fact that the dual notion of a limit is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology.
Another example is given by currying, which tells us that for any object X, a map \( X \times I \to Y \) is the same as a map \( X \to Y^I \) , where \( Y^I \) is the exponential object, given by all maps from I to Y . In the case of topological spaces, if we take I to be the unit interval, this leads to a duality between \( X \times I \) and \( Y^I \) which then gives a duality between the reduced suspension \( \Sigma X \) which is a quotient of \( X \times I \) and the loop space \( \Omega \) Y which is a subspace of \( Y ^ I \) . This then leads to the adjoint relation \( \langle \Sigma X, Y \rangle = \langle X, \Omega Y \rangle \) which allows the study of spectra which give rise to cohomology theories.
We can also directly relate fibrations and cofibrations: a fibration \( p \colon E \to B \) is defined by having the homotopy lifting property, represented by the following diagram
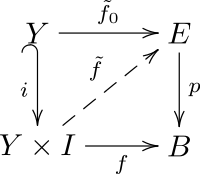
and a cofibration \( i \colon A \to X \) is defined by having the dual homotopy extension property, represented by dualising the previous diagram:
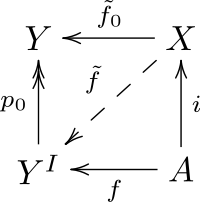
The above considerations also apply when looking at the sequences associated to a fibration or a cofibration, as given a fibration \( F \to E \to B \) we get the sequence
\( \cdots \to \Omega^2 B \to \Omega F \to \Omega E \to \Omega B \to F \to E \to B \, \)
and given a cofibration \( A \to X \to X/A \) we get the sequence
\( A \to X \to X/A \to \Sigma A \to \Sigma X \to \Sigma \left (X/A \right ) \to \Sigma^2 A \to \cdots. \, \)
This also allows us to relate homotopy and cohomology: we know that homotopy groups are homotopy classes of maps from the n-sphere to our space, written \( \pi_n(X,p) \cong \langle S^n,X \rangle \) , and we know that the sphere has a single nonzero (reduced) cohomology group. On the other hand, cohomology groups are homotopy classes of maps to spaces with a single nonzero homotopy group. This is given by the Eilenberg–MacLane spaces K(G,n) and the relation \( H^n(X;G) \cong \langle X,K(G,n) \rangle \) .
References
Hatcher, Allen (2002), Algebraic Topology, Cambridge: Cambridge University Press, ISBN 0-521-79540-0.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

