.
Fagnano's problem
In geometry, Fagnano's problem is an optimization problem that was first stated by Giovanni Fagnano in 1775:
For a given acute triangle determine the inscribed triangle of minimal perimeter.
The orthic triangle, with vertices at the base points of the altitudes of the given triangle, has the smallest perimeter of all triangles inscribed into an acute triangle, hence it is the solution of Fagnano's problem. Fagnano's original proof used calculus methods and an intermediate result given by his father Giulio Carlo de' Toschi di Fagnano. Later however several geometric proofs were discovered as well, amongst others by Hermann Schwarz and Lipót Fejér. These proofs use the geometrical properties of reflections to determine some minimal path representing the perimeter.
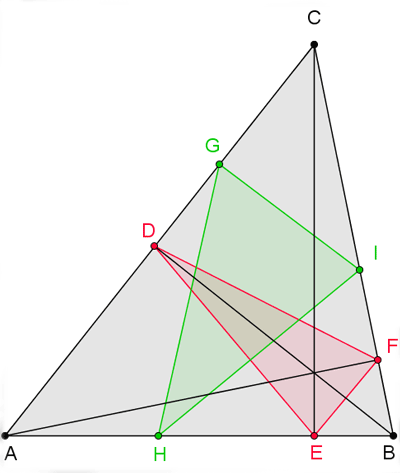
Orthic triangle: Triangle DEF
inscribed triangles: Triangle DEF Triangle GHI
|DE|+|EF|+|FD| less or equal |GH|+|HI|+|IG| (*)
References
Heinrich Dörrie: 100 Great Problems of Elementary Mathematics: Their History and Solution. Dover Publications 1965, p. 359-360. ISBN 0-486-61348-8, problem 90 (restricted online version (Google Books))
Paul J. Nahin: When Least is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible. Princeton University Press 2004, ISBN 0-691-07078-4, p. 67
Coxeter, H. S. M.; Greitzer, S. L.:Geometry Revisited. Washington, DC: Math. Assoc. Amer. 1967, pp. 88–89.
External links
Fagnano's problem at cut-the-knot
Fagnano's problem in the Encyclopaedia of Mathematics
Fagnano's problem at a website for triangle geometry
Weisstein, Eric W., "Fagnano's problem", MathWorld.
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

