Fermat's spiral

Fermat's spiral (also known as a parabolic spiral) follows the equation

\( r = \pm\theta^{1/2}\, \)

in polar coordinates (the more general Fermat's spiral follows r 2 = a 2θ.) It is a type of Archimedean spiral.[1]

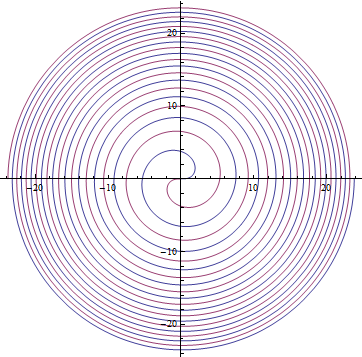
Examples: Fermat's spiral , using Mathematica : PolarPlot[ {\( 3t^{1/2} ,-3t^{1/2} \) }, {t,0,20Pi}]

In disc phyllotaxis (sunflower, daisy), the mesh of spirals occurs in Fibonacci numbers because divergence (angle of succession in a single spiral arrangement) approaches the golden ratio. The shape of the spirals depends on the growth of the elements generated sequentially. In mature-disc phyllotaxis, when all the elements are the same size, the shape of the spirals is that of Fermat spirals—ideally. That is because Fermat's spiral traverses equal annuli in equal turns. The full model proposed by H Vogel in 1979[2] is

\( r = c \sqrt{n}, \)

\( \theta = n \times 137.508^\circ, \)

where θ is the angle, r is the radius or distance from the center, and n is the index number of the floret and c is a constant scaling factor. The angle 137.508° is the golden angle which is approximated by ratios of Fibonacci numbers.[3] The Fermat's spiral has also be found to be an efficient layout for the mirrors of concentrated solar power plants.[4]
The pattern of florets produced by Vogel's model (central image). The other two images show the patterns for slightly different values of the angle.
References

^ Weisstein, Eric W., "Fermat Spiral" from MathWorld.
^ Vogel, H (1979). "A better way to construct the sunflower head". Mathematical Biosciences 44 (44): 179–189. doi:10.1016/0025-5564(79)90080-4
^ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8. http://algorithmicbotany.org/papers/#webdocs.
^ Mitsos, Alexander (December 2011). "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout". Solar Energy. doi:10.1016/j.solener.2011.12.007

J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 31,186. ISBN 0-486-60288-5.

External links

Online exploration using JSXGraph (JavaScript)