.
Hippopede
In geometry, a hippopede (from ἱπποπέδη meaning "horse fetter" in ancient Greek) is a plane curve determined by an equation of the form
\( (x^2+y^2)^2=cx^2+dy^2, \)
where it is assumed that c>0 and c>d since the remaining cases either reduce to a single point or can be put into the given form with a rotation. Hippopedes are bicircular rational algebraic curves of degree 4 and symmetric with respect to both the x and y axes. When d>0 the curve has an oval form and is often known as an oval of Booth, and when d<0 the curve resembles a sideways figure eight, or lemniscate, and is often known as a lemniscate of Booth, after James Booth (1810–1878) who studied them. Hippopedes were also investigated by Proclus (for whom they are sometimes called Hippopedes of Proclus) and Eudoxus. For d = −c, the hippopede corresponds to the lemniscate of Bernoulli.
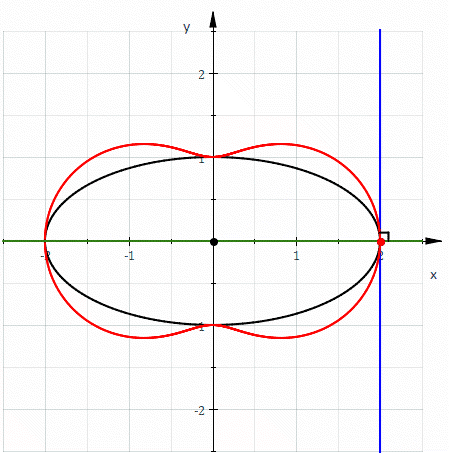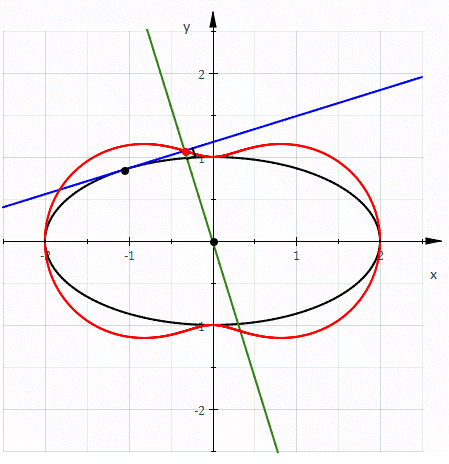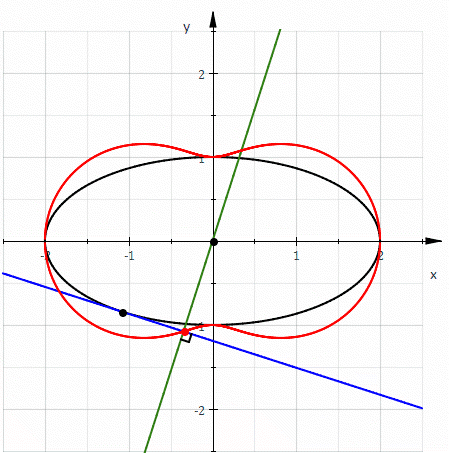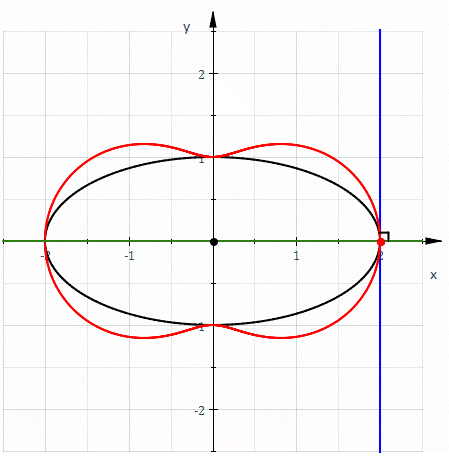
Hippopede (red) given as the pedal curve of an ellipse (black). The equation of the hippopede is 4x2+y2=(x2+y2)2. (*)
Definition as spiric sections
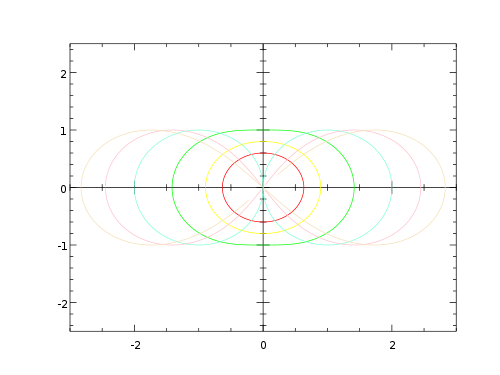
Hippopedes with a = 1, b = 0.1, 0.2, 0.5, 1.0, 1.5, and 2.0.
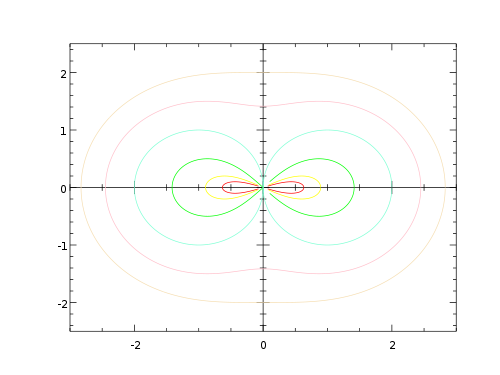
Hippopedes with b = 1, a = 0.1, 0.2, 0.5, 1.0, 1.5, and 2.0.
Hippopedes can be defined as the curve formed by the intersection of a torus and a plane, where the plane is parallel to the axis of the torus and tangent to it on the interior circle. Thus it is a spiric section which in turn is a type of toric section.
If a circle with radius a is rotated about an axis at distance b from its center, then the equation of the resulting hippopede in polar coordinates
\( r^2 = 4 b (a- b \sin^{2} \theta)\, \)
or in Cartesian coordinates
\( (x^2+y^2)^2+4b(b-a)(x^2+y^2)=4b^2x^2. \)
Note that when a>b the torus intersects itself, so it does not resemble the usual picture of a torus.
See also
List of curves
References
Lawrence JD. (1972) Catalog of Special Plane Curves, Dover. Pp. 145–146.
Booth J. A Treatise on Some New Geometrical Methods, Longmans, Green, Reader, and Dyer, London, Vol. I (1873) and Vol. II (1877).
Weisstein, Eric W., "Hippopede" from MathWorld.
"Hippopede" at 2dcurves.com
"Courbes de Booth" at Encyclopédie des Formes Mathématiques Remarquables
External links
"The Hippopede of Proclus" at The National Curve Bank
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

