Holt graph

In the mathematical field of graph theory, the Holt graph or Doyle graph is the smallest half-transitive graph, that is, the smallest example of a vertex-transitive and edge-transitive graph which is not also symmetric.[1][2] Such graphs are not common.[3] It is named after Peter G. Doyle and Derek F. Holt, who discovered the same graph independently in 1976[4] and 1981[5] respectively.

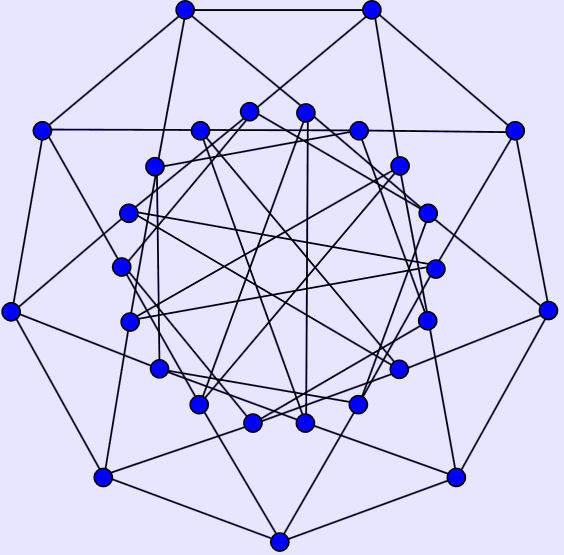
Holt Graph. In the Holt graph, all vertices are equivalent, and all edges are equivalent, but edges are not necessarily equivalent to their inverses.(*)

The Holt Graph has diameter 3, radius 3 and girth 5, chromatic number 3, chromatic index 5 and is Hamiltonian with 98,472 distinct Hamiltonian cycles.[6] It is also a 4-vertex-connected and a 4-edge-connected graph.

It has an automorphism group of order 54 automorphisms.[6] This is a smaller group than a symmetric graph with the same number of vertices and edges would have. The graph drawing on the right highlights this, in that it lacks reflectional symmetry.

The characteristic polynomial of the Holt graph is

(x^3-6x+2)^6(x+2)^4(x-1)^4(x-4).\

References

^ Doyle, P. "A 27-Vertex Graph That Is Vertex-Transitive and Edge-Transitive But Not L-Transitive." October 1998. [1]
^ Alspach, Brian; Marušič, Dragan; Nowitz, Lewis (1994), "Constructing Graphs which are ½-Transitive", Journal of the Australian Mathematical Society (Series A) 56 (3): 391–402, doi:10.1017/S1446788700035564.
^ Jonathan L. Gross, Jay Yellen, Handbook of Graph Theory, CRC Press, 2004, ISBN 1584880902, p. 491.
^ Doyle, P. G. (1976), On Transitive Graphs, Senior Thesis, Harvard College. As cited by MathWorld.
^ Holt, Derek F. (1981), "A graph which is edge transitive but not arc transitive", Journal of Graph Theory 5 (2): 201–204, doi:10.1002/jgt.3190050210.
^ a b Weisstein, Eric W., "Doyle Graph" from MathWorld.

Mathematics Encyclopedia