Horton graph

In the mathematical field of graph theory, the Horton graph or Horton 96-graph is a 3-regular graph with 96 vertices and 144 edges discovered by Joseph Horton.[1] Published by Bondy and Murty in 1976, it provides a counterexample to the Tutte conjecture that every cubic 3-connected bipartite graph is Hamiltonian.[2][3]

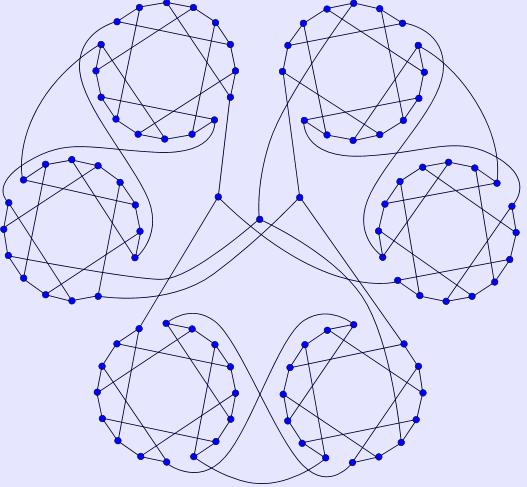
Horton graph (*)

After the Horton graph, a number of smaller counterexamples to the Tutte conjecture were found. Among them are a 92 vertices graph by Horton published in 1982, a 78 vertices graph by Owens published in 1983, and the two Ellingham-Horton graphs (54 and 78 vertices).[4][5]

The first Ellingham-Horton graph was published by Ellingham in 1981 and was of order 78.[6] At that time, it was the smallest know counterexample to the Tutte conjecture. The second one was published by Ellingham and Horton in 1983 and was of order 54.[7] No smaller non-hamiltonian cubic 3-connected bipartite graph is currently known.

As a non-hamiltonian cubic graph with many long cycles, the Horton graph provides good benchmark for programs that search for Hamiltonian cycles.[8]

The Horton graph has chromatic number 2, chromatic index 3, radius 10, diameter 10 and girth 6. It is also a 3-edge-connected graph.
Algebraic properties

The automorphism group of the Horton graph is of order 96 and is isomorphic to Z/2Z×Z/2Z×S₄, the direct product of the cyclic group Z/2Z with itself and the symmetric group S₄.

The characteristic polynomial of the Horton graph is : \( (x-3) (x-1)^{14} x^4 (x+1)^{14} (x+3) (x^2-5)^3 (x^2-3)^{11}(x^2-x-3) (x^2+x-3) (x^{10}-23 x^8+188 x^6-644 x^4+803 x^2-101)^2 (x^{10}-20 x^8+143 x^6-437 x^4+500 x^2-59). \)

Gallery

The chromatic number of the Horton graph is 2.

The chromatic index of the Horton graph is 3.

The Ellingham-Horton 54-graph, a smaller counterexample to the Tutte conjecture.

References

^ Weisstein, Eric W., "Horton graph" from MathWorld.
^ Tutte, W. T. "On the 2-Factors of Bicubic Graphs." Disc. Math. 1, 203-208, 1971/72.
^ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 240, 1976.
^ Horton, J. D. "On Two-Factors of Bipartite Regular Graphs." Disc. Math. 41, 35-41, 1982.
^ Owens, P. J. "Bipartite Cubic Graphs and a Shortness Exponent." Disc. Math. 44, 327-330, 1983.
^ Ellingham, M. N. "Non-Hamiltonian 3-Connected Cubic Partite Graphs."Research Report No. 28, Dept. of Math., Univ. Melbourne, Melbourne, 1981.
^ Ellingham, M. N. and Horton, J. D. "Non-Hamiltonian 3-Connected Cubic Bipartite Graphs." J. Combin. Th. Ser. B 34, 350-353, 1983.
^ V. Ejov, N. Pugacheva, S. Rossomakhine, P. Zograf "An effective algorithm for the enumeration of edge colorings and Hamiltonian cycles in cubic graphs" arXiv:math/0610779v1.

Mathematics Encyclopedia