.

In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface. Equivalently, the codimension of a hypersurface is one. For example, the n-sphere in R^{n + 1} is called a hypersphere. Hypersurfaces occur frequently in multivariable calculus as level sets.

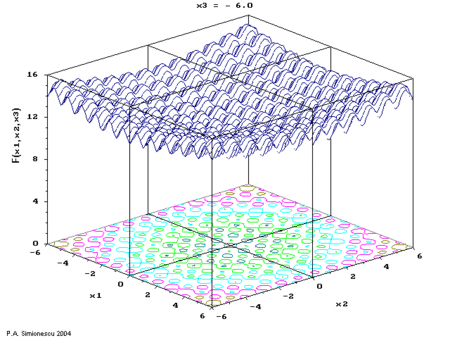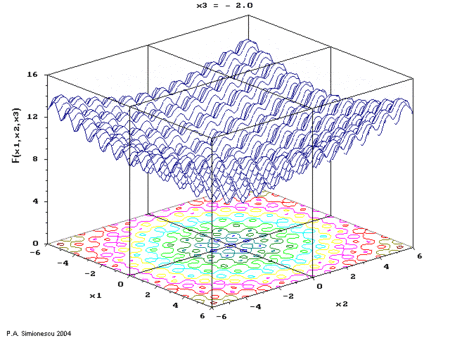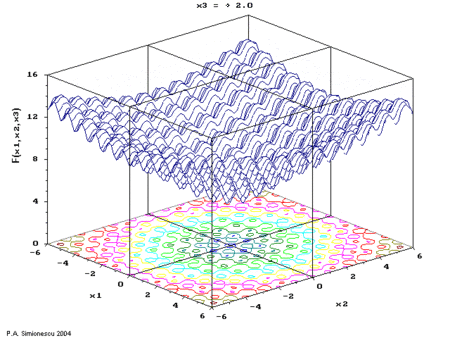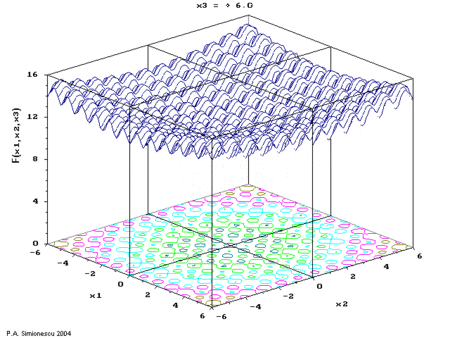
Ackley's function of three variables, with time the 3rd variable.

In Rⁿ, every closed hypersurface is orientable.^[1] Every connected compact hypersurface is a level set,^[2] and separates Rⁿ in two connected components,^[2] which is related to the Jordan–Brouwer separation theorem.

In algebraic geometry, a hypersurface in projective space of dimension n is an algebraic set (algebraic variety) that is purely of dimension n − 1. It is then defined by a single equation f(x₁,x₂,...,x_n) = 0, a homogeneous polynomial in the homogeneous coordinates.

Thus, it generalizes those algebraic curves f(x₁,x₂) = 0 (dimension one), and those algebraic surfaces f(x₁,x₂,x₃) = 0 (dimension two), when they are defined by homogeneous polynomials.

A hypersurface may have singularities, so not a submanifold in the strict sense. "Primal" is an old term for an irreducible hypersurface.

.

Hyperplane