Japanese theorem for cyclic polygons

In geometry, the Japanese theorem states that no matter how one triangulates a cyclic polygon, the sum of inradii of triangles is constant.[1]:p. 193

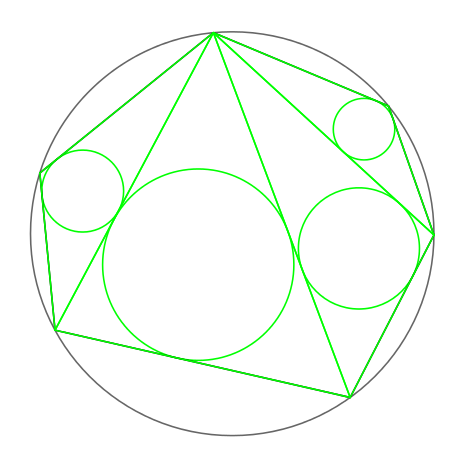
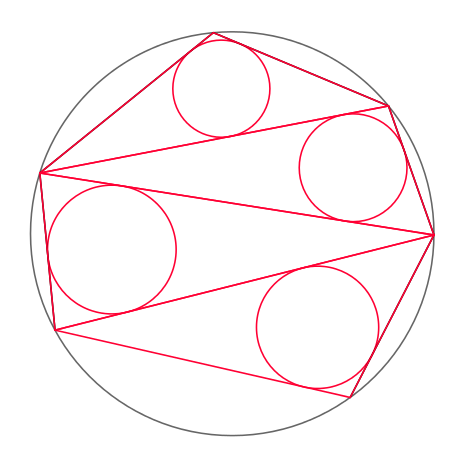
sum of the radii of the green circles = sum of the radii of the red circles

Conversely, if the sum of inradii independent from the triangulation, then the polygon is cyclic. The Japanese theorem follows from the Carnot's theorem; it is a Sangaku problem.

This theorem also follows from a simple extension of the Japanese theorem for cyclic quadrilaterals. That theorem shows that a rectangle is formed by the two pairs of incenters corresponding to the two possible triangulations of the quadrilateral. The steps of this theorem require nothing beyond basic constructive Euclidean geometry.

With the additional construction of a parallelogram having sides parallel to the diagonals, and tangent to the corners of the rectangle of incenters, the quadrilateral case of the concyclic polygon theorem can be proved in a few steps. The equality of the sums of the radii of the two pairs is equivalent to the condition that the constructed parallelogram be a rhombus, and this is easily shown in the construction.

Also, it's readily shown that the quadrilateral case suffices to prove the general case of the concyclic polygon theorem. The quadrilateral rule can be applied to quadrilateral components of a general partition of a cyclic polygon, and repeated application of the rule, which "flips" one diagonal, will generate all the possible partitions from any given partition, with each "flip" preserving the sum of the inradii. Hence the concyclic polygon theorem considered here can be regarded as a corollary of the extended cyclic quadrilateral theorem.
See also

Carnot's theorem, which is used in a proof of the theorem above

Equal incircles theorem

Tangent lines to circles

References

Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).

External links

Mangho Ahuja, Wataru Uegaki, Kayo Matsushita: In Search of the Japanese Theorem
Japanese theorem at Mathworld
Japanese Theorem interactive demonstration at the C.a.R. website
Wataru Uegaki: "Japanese Theoremの起源と歴史" (On the Origin and History of the Japanese Theorem) http://hdl.handle.net/10076/4917