Jordan's inequality

In mathematics, Jordan's inequality, named after Camille Jordan, states that

\( \frac{2}{\pi}x\leq \sin{x} \leq x\text{ for }x \in \left[0,\frac{\pi}{2}\right]\).

It can be proven through the geometry of circles (see drawing).[1]

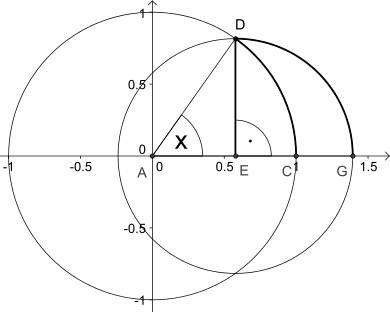
unit circle with angle x and a second circle with radius |\( EG|=\sin(x) \) around E. \( \begin{align}&|DE|\leq|\widehat{DC}|\leq|\widehat{DG}|\\ \Leftrightarrow &\sin(x) \leq x \leq\tfrac{\pi}{2}\sin(x)\\ \Rightarrow &\tfrac{2}{\pi}x \leq \sin(x)\leq x \end{align} \)

Notes

http://planetmath.org/encyclopedia/ProofOfJordansInequality.html

Further reading

Serge Colombo: Holomorphic Functions of One Variable. Taylor & Francis 1983, ISBN 0677059507, p. 167-168 (online copy)
Da-Wei Niu, Jian Cao, Feng Qi: Generealizations of Jordan's Inequality and Concerned Relations. U.P.B. Sci. Bull., Series A, Volume 72, Issue 3, 2010, ISSN 1223-7027
Peng Qi: Jordan's Inequality: Refinements, Generealizations, Applications and related Problems. RGMIA Res Rep Coll (2006), Volume: 9, Issue: 3, Pages: 243–259
Meng-Kuang Kuo: Refinements of Jordan's inequality. Journal of Inequalities and Applications 2011, 2011:130, doi:10.1186/1029-242X-2011-130

External links

Jordan's inequality at PlanetMath
Weisstein, Eric W., "Jordan's inequality", MathWorld.