Seifert fiber space

A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle (circle bundle) over a 2-dimensional orbifold. Most "small" 3-manifolds are Seifert fiber spaces, and they account for all compact oriented manifolds in 6 of the 8 Thurston geometries of the geometrization conjecture.

Definition

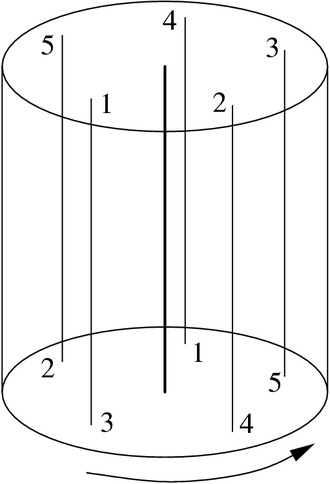
A standard fibered torus corresponding to (5,2) is obtained by gluing the top of the cylinder to the bottom by a 3/5 rotation counterclockwise.

A Seifert manifold is a closed 3-manifold together with a decomposition into a disjoint union of circles (called fibers) such that each fiber has a tubular neighborhood that forms a standard fibered torus.

A standard fibered torus corresponding to a pair of coprime integers (a,b) with a>0 is the surface bundle of the automorphism of a disk given by rotation by an angle of 2πb/a (with the natural fibering by circles). If a = 1 the middle fiber is called ordinary, while if a>1 the middle fiber is called exceptional. A compact Seifert fiber space has only a finite number of exceptional fibers.

The set of fibers forms a 2-dimensional orbifold, denoted by B and called the base -also called the orbit surface- of the fibration. It has an underlying 2-dimensional surface B0, but may have some special orbifold points corresponding to the exceptional fibers.

The definition of Seifert fibration can be generalized in several ways. The Seifert manifold is often allowed to have a boundary (also fibered by circles, so it is a union of tori). When studying non-orientable manifolds, it is sometimes useful to allow fibers to have neighborhoods that look like the surface bundle of a reflection (rather than a rotation) of a disk, so that some fibers have neighborhoods looking like fibered Klein bottles, in which case there may be one-parameter families of exceptional curves. In both of these cases, the base B of the fibration usually has a non-empty boundary.
Classification

Seifert classified all closed Seifert fibrations in terms of the following invariants. Seifert manifolds are denoted by symbols

\( \{b, (\varepsilon,g);(a_1,b_1),\dots,(a_r,b_r)\}\, \)

where: \( \varepsilon \) is one of the 6 symbols: \( o_1,o_2,n_1,n_2,n_3,n_4\,, \) (or Oo, No, NnI, On, NnII, NnIII in Seifert's original notation) meaning:

o₁ if B is orientable and M is orientable.

o₂ if B is orientable and M is not orientable.

n₁ if B is not orientable and M is not orientable and all generators of π₁(B) preserve orientation of the fiber.

n₂ if B is not orientable and M is orientable, so all generators of π₁(B) reverse orientation of the fiber.

n₃ if B is not orientable and M is not orientable and g≥ 2 and exactly one generator of π₁(B) preserves orientation of the fiber.

n₄ if B is not orientable and M is not orientable and g≥ 3 and exactly two generators of π₁(B) preserve orientation of the fiber.

g is the genus of the underlying 2-manifold of the orbit surface.

b is an integer, normalized to be 0 or 1 if M is not orientable and normalized to be 0 if in addition some a_'i is 2.

(a₁,b₁),...,(a_r,b_r) are the pairs of numbers determining the type of each of the r exceptional orbits. They are normalized so that 0<b_i<a_i when M is orientable, and 0<b_i≤a_i/2 when M is not orientable.

The Seifert fibration of the symbol

\( \{b, (\epsilon,g);(a_1,b_1),...,(a_r,b_r)\} \)

can be constructed from that of symbol

\(\{0, (\epsilon,g);\} \)

by using surgery to add fibers of types b and b_i/a_i.

If we drop the normalization conditions then the symbol can be changed as follows:

• Changing the sign of both a_i and b_i has no effect.
• Adding 1 to b and subtracting a_i from b_i has no effect. (In other words we can add integers to each of the rational numbers (b, b₁/a₁, ..., b_r/a_r provided that their sum remains constant.)
• If the manifold is not orientable, changing the sign of b_i' has no effect.
• Adding a fiber of type (1,0) has no effect.

Every symbol is equivalent under these operations to a unique normalized symbol. When working with unnormalized symbols, the integer b can be set to zero by adding a fiber of type (1, b).

Two closed Seifert oriented or non-orientable fibrations are isomorphic as oriented or non-orientable fibrations if and only if they have the same normalized symbol. However, it is sometimes possible for two Seifert manifolds to be homeomorphic even if they have different normalized symbols, because a few manifolds (such as lens spaces) can have more than one sort of Seifert fibration. Also an oriented fibration under a change of orientation becomes the Seifert fibration whose symbol has the sign of all the bs changed, which after normalization gives it the symbol

\( \{-b-r, (\epsilon,g);(a_1,a_1-b_1),...,(a_r,a_r-b_r)\} \)where χ(B0) is the usual Euler characteristic of the underlying topological surface B0 of the orbifold B. The behavior of M depends largely on the sign of the orbifold Euler characteristic of B.

and it is homeomorphic to this as an unoriented manifold.

The sum b + Σb_i/a_i is an invariant of oriented fibrations, which is zero if and only if the fibration becomes trivial after taking a finite cover of B.

The orbifold Euler characteristic χ(B) of the orbifold B is given by

χ(B) = χ(B₀) − Σ(1−1/a_i)

where χ(B₀) is the usual Euler characteristic of the underlying topological surface B₀ of the orbifold B. The behavior of M depends largely on the sign of the orbifold Euler characteristic of B.

Fundamental group

The fundamental group of M fits into the exact sequence

\(\pi_1(S^1)\rightarrow\pi_1(M)\rightarrow\pi_1(B)\rightarrow1 \)

where π₁(B) is the orbifold fundamental group of B (which is not the same as the fundamental group of the underlying topological manifold). The image of group π₁(S¹) is cyclic, normal, and generated by the element h represented by any regular fiber, but the map from π₁(S¹) to π₁(M) is not always injective.

The fundamental group of M has the following presentation by generators and relations:

B orientable:

\( \langle u_1,v_1,...u_g,v_g,q_1,...q_r,h|u_ih=h^{\epsilon}u_i, v_ih=h^{\epsilon}v_i,q_ih=hq_i, q_j^{a_j}h^{b_j}=1, q_1...q_r[u_1,v_1]...[u_g,v_g]=h^b\rangle \)

where ε is 1 for type o1, and is −1 for type o2.

B non-orientable:

\( \langle v_1,...,v_g,q_1,...q_r,h| v_ih=h^{\epsilon_i}v_i,q_ih=hq_i, q_j^{a_j}h^{b_j}=1, q_1...q_rv_1^2...v_g^2=h^b\rangle \)

where ε_i is 1 or −1 depending on whether the corresponding generator v_i preserves or reverses orientation of the fiber. (So ε_i are all 1 for type n₁, all −1 for type n₂, just the first one is one for type n₃, and just the first two are one for type n₄.)

Positive orbifold Euler characteristic

The normalized symbols of Seifert fibrations with positive orbifold Euler characteristic are given in the list below. These Seifert manifolds often have many different Seifert fibrations. They have a spherical Thurston geometry if the fundamental group is finite, and an S²×R Thurston geometry if the fundamental group is infinite. Equivalently, the geometry is S²×R if the manifold is non-orientable or if b + Σb_i/a_i= 0, and spherical geometry otherwise.

{b; (o₁, 0);} (b integral) is S²×S¹ for b=0, otherwise a lens space L(b,1). ({1; (o₁, 0);} =L(1,1) is the 3-sphere.)

{b; (o₁, 0);(a₁, b₁)} (b integral) is the Lens space L(ba₁+b₁,a₁).

{b; (o₁, 0);(a₁, b₁), (a₂, b₂)} (b integral) is S²×S¹ if ba₁a₂+a₁b₂+a₂b₁ = 0, otherwise the lens space L(ba₁a₂+a₁b₂+a₂b₁, ma₂+nb₂) where ma₁ − n(ba₁ +b₁) = 1.

{b; (o₁, 0);(2, 1), (2, 1), (a₃, b₃)} (b integral) This is the Prism manifold with fundamental group of order 4a₃|(b+1)a₃+b₃| and first homology group of order 4|(b+1)a₃+b₃|.

{b; (o₁, 0);(2, 1), (3, b₂), (3, b₃)} (b integral) The fundamental group is a central extension of the tetrahedral group of order 12 by a cyclic group.

{b; (o₁, 0);(2, 1), (3, b₂), (4, b₃)} (b integral) The fundamental group is the product of a cyclic group of order |12b+6+4b₂ + 3b₃| and a double cover of order 48 of the octahedral group of order 24.

{b; (o₁, 0);(2, 1), (3, b₂), (5, b₃)} (b integral) The fundamental group is the product of a cyclic group of order m=|30b+15+10b₂ +6b₃| and the order 120 perfect double cover of the icosahedral group. The manifolds are quotients of the Poincaré sphere by cyclic groups of order m. In particular {−1; (o₁, 0);(2, 1), (3, 1), (5, 1)} is the Poincaré sphere.

{b; (n₁, 1);} (b is 0 or 1.) These are the non-orientable 3-manifolds with S²×R geometry. If b is even this is homeomorphic to the projective plane times the circle, otherwise it is homeomorphic to a surface bundle associated to an orientation reversing automorphism of the 2-sphere.

{b; (n₁, 1);(a₁, b₁)} (b is 0 or 1.) These are the non-orientable 3-manifolds with S²×R geometry. If ba₁+b₁ is even this is homeomorphic to the projective plane times the circle, otherwise it is homeomorphic to a surface bundle associated to an orientation reversing automorphism of the 2-sphere.

{b; (n₂, 1);} (b integral.) This is the Prism manifold with fundamental group of order 4|b| and first homology group of order 4, except for b=0 when it is a sum of two copies of real projective space, and |b|=1 when it is the lens space with fundamental group of order 4.

{b; (n₂, 1);(a₁, b₁)} (b integral.) This is the (unique) Prism manifold with fundamental group of order 4a₁|ba₁ + b₁| and first homology group of order 4a₁.

Zero orbifold Euler characteristic

The normalized symbols of Seifert fibrations with zero orbifold Euler characteristic are given in the list below. The manifolds have Euclidean Thurston geometry if they are non-orientable or if b + Σb_i/a_i= 0, and nil geometry otherwise. Equivalently, the manifold has Euclidean geometry if and only if its fundamental group has an abelian group of finite index. There are 10 Euclidean manifolds, but four of them have two different Seifert fibrations. All surface bundles associated to automorphisms of the 2-torus of trace 2, 1, 0, −1, or −2 are Seifert fibrations with zero orbifold Euler characteristic (the ones for other (Anosov) automorphisms are not Seifert fiber spaces, but have sol geometry). The manifolds with nil geometry all have a unique Seifert fibration, and are characterized by their fundamental groups. The total spaces are all acyclic.

{b; (o₁, 0); (3, b₁), (3, b₂), (3, b₃)}    (b integral, b_i is 1 or 2) For b + Σb_i/a_i= 0 this is an oriented Euclidean 2-torus bundle over the circle, and is the surface bundle associated to an order 3 (trace −1) rotation of the 2-torus.

{b; (o₁, 0); (2,1), (4, b₂), (4, b₃)}    (b integral, b_i is 1 or 3) For b + Σb_i/a_i= 0 this is an oriented Euclidean 2-torus bundle over the circle, and is the surface bundle associated to an order 4 (trace 0) rotation of the 2-torus.

{b; (o₁, 0); (2, 1), (3, b₂), (6, b₃)}    (b integral, b₂ is 1 or 2, b₃ is 1 or 5) For b + Σb_i/a_i= 0 this is an oriented Euclidean 2-torus bundle over the circle, and is the surface bundle associated to an order 6 (trace 1) rotation of the 2-torus.

{b; (o₁, 0); (2, 1), (2, 1), (2, 1), (2, 1)}    (b integral) These are oriented 2-torus bundles for trace −2 automorphisms of the 2-torus. For b=−2 this is an oriented Euclidean 2-torus bundle over the circle (the surface bundle associated to an order 2 rotation of the 2-torus) and is homeomorphic to {0; (n₂, 2);}.

{b; (o₁, 1); }   (b integral) This is an oriented 2-torus bundle over the circle, given as the surface bundle associated to a trace 2 automorphism of the 2-torus. For b=0 this is Euclidean, and is the 3-torus (the surface bundle associated to the identity map of the 2-torus).

{b; (o₂, 1); }   (b is 0 or 1) Two non-orientable Euclidean Klein bottle bundles over the circle. The first homology is Z+Z+Z/2Z if b=0, and Z+Z if b=1. The first is the Klein bottle times S¹ and other is the surface bundle associated to a Dehn twist of the Klein bottle. They are homeomorphic to the torus bundles {b; (n₁, 2);}.

{0; (n₁, 1); (2, 1), (2, 1)}   Homeomorphic to the non-orientable Euclidean Klein bottle bundle {1; (n₃, 2);}, with first homology Z + Z/4Z.

{b; (n₁, 2); }   (b is 0 or 1) These are the non-orientable Euclidean surface bundles associated with orientation reversing order 2 automorphisms of a 2-torus with no fixed points. The first homology is Z+Z+Z/2Z if b=0, and Z+Z if b=1. They are homeomorphic to the Klein bottle bundles {b; (o₂, 1);}.

{b; (n₂, 1); (2, 1), (2, 1)}   (b integral) For b=−1 this is oriented Euclidean.

{b; (n₂, 2); }   (b integral) For b=0 this is an oriented Euclidean manifold, homeomorphic to the 2-torus bundle {−2; (o₁, 0); (2, 1), (2, 1), (2, 1), (2, 1)} over the cicle associated to an order 2 rotation of the 2-torus.

{b; (n₃, 2); }   (b is 0 or 1) The other two non-orientable Euclidean Klein bottle bundles. The one with b = 1 is homeomorphic to {0; (n₁, 1); (2, 1), (2, 1)}. The first homology is Z+Z/2Z+Z/2Z if b=0, and Z+Z/4Z if b=1. These two Klein bottle bundle are surface bundles associated to the y-homeomorphism and the product of this and the twist.

Negative orbifold Euler characteristic

This is the general case. All such Seifert fibrations are determined up to isomorphism by their fundamental group. The total spaces are aspherical (in other words all higher homotopy groups vanish). They have Thurston geometries of type the universal cover of SL₂(R), unless some finite cover splits as a product, in which case they have Thurston geometries of type H₂×R. This happens if the manifold is non-orientable or b + Σb_i/a_i= 0.

References

A.V. Chernavskii (2001), "Seifert fibration", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Herbert Seifert, Topologie dreidimensionaler gefaserter Räume, Acta Math. 60 (1933) 147-238 (There is a translation by W. Heil, published by Florida state university in 1976 and found in: Herbert Seifert, William Threlfall, Seifert and Threllfall: a textbook of topology, Pure and Applied Mathematics, Academic Press Inc (1980), vol. 89.)
Peter Orlik Seifert manifolds, Lecture notes in mathematics 291, Springer (1972).
Frank Raymond Classification of the actions of the circle on 3-manifolds, Trans. Amer.Math. Soc 31, (1968) 51-87.
William H. Jaco, Lectures on 3-manifold topology ISBN 0-8218-1693-4
William H. Jaco, Peter B. Shalen Seifert Fibered Spaces in Three Manifolds: Memoirs Series No. 220 (Memoirs of the American Mathematical Society; v. 21, no. 220) ISBN 0-8218-2220-9
Matthew G. Brin Seifert fibered 3-manifolds. Course notes.
John Hempel, 3-manifolds, American Mathematical Society, ISBN 0-8218-3695-1
Peter Scott The geometries of 3-manifolds. (errata) Bull. London Math. Soc. 15 (1983), no. 5, 401-487.

Mathematics Encyclopedia