.
Spherical cap
In geometry, a spherical cap or spherical dome is a portion of a sphere cut off by a plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.
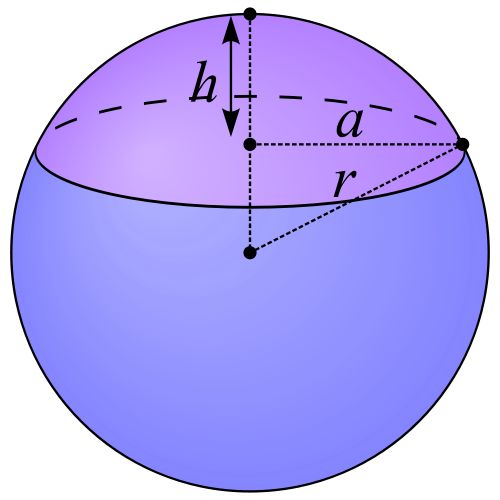
The spherical cap is the purple section.
Volume and surface area
If the radius of the base of the cap is a, and the height of the cap is h, then the volume of the spherical cap is
\( V = \frac{\pi h}{6} (3a^2 + h^2), \)
and the curved surface area of the spherical cap is
\( A = 2 \pi r h. \)
The relationship between h and r is irrelevant as long as 0 ≤ h ≤ 2r. The blue section of the illustration is also a spherical cap.
The parameters a, h and r are not independent:
\( r^2 = (r-h)^2 + a^2 = r^2 +h^2 -2rh +a^2, \)
\( r = \frac {a^2 + h^2}{2h}. \)
Substituting this into the area formula gives:
\( A = 2 \pi \frac{(a^2 + h^2)}{2h} h = \pi (a^2 + h^2). \)
Note also that in the upper hemisphere of the diagram, \scriptstyle \(h = r - \sqrt{r^2 - a^2} \), and in the lower hemisphere \(\scriptstyle h = r + \sqrt{r^2 - a^2} \); hence in either hemisphere \( \scriptstyle a = \sqrt{h(2r-h)} \) and so an alternative expression for the volume is
\( V = \frac {\pi h^2}{3} (3r-h). \)
Application
The volume of all points which are in at least one of two intersecting spheres of radii r1 and r2 is [1]
\( V = V^{(1)}-V^{(2)}, \)
where
\( V^{(1)} = \frac{4\pi}{3}r_1^3 +\frac{4\pi}{3}r_2^3 \)
is the total of the two isolated spheres, and
\( V^{(2)} = \frac{\pi h_1^2}{3}(3r_1-h_1)+\frac{\pi h_2^2}{3}(3r_2-h_2) \)
the sum of the two spherical caps of the intersection. If d <r1+r2 is the distance between the two sphere centers, elimination of the variables h1 and h2 leads to[2] [3]
\( V^{(2)} = \frac{\pi}{12d}(r_1+r_2-d)^2[d^2+2d(r_1+r_2)-3(r_1-r_2)^2]. \)
Generalizations
Sections of other solids
The spheroidal dome is obtained by sectioning off a portion of a spheroid so that the resulting dome is circularly symmetric (having an axis of rotation), and likewise the ellipsoidal dome is derived from the ellipsoid.
Hyperspherical cap
Generally, the n-dimensional volume of a hyperspherical cap of height h and radius r in n-dimensional Euclidean space is given by [4]
\( V = \frac{\pi ^ {\frac{n-1}{2}}\, r^{n}}{\,\Gamma \left ( \frac{n+1}{2} \right )} \int\limits_{0}^{\arccos\left(\frac{r-h}{r}\right)}\sin^n (t) \,\mathrm{d}t \)
where \(\Gamma \) (the gamma function) is given by \( \Gamma(z) = \int_0^\infty t^{z-1} \mathrm{e}^{-t}\,\mathrm{d}t \).
The formula for V can be expressed in terms of the volume of the unit n-ball \(C_{n}={\scriptstyle \pi^{n/2}/\Gamma[1+\frac{n}{2}]} \) and the hypergeometric function \({}_{2}F_{1} \)or the regularized incomplete beta function \( I_x(a,b)as \)
\( V = C_{n} \, r^{n} \left( \frac{1}{2}\, - \,\frac{r-h}{r} \,\frac{\Gamma[1+\frac{n}{2}]}{\sqrt{\pi}\,\Gamma[\frac{n+1}{2}]} {\,\,}_{2}F_{1}\left(\tfrac{1}{2},\tfrac{1-n}{2};\tfrac{3}{2};\left(\tfrac{r-h}{r}\right)^{2}\right)\right) =\frac{1}{2}C_{n} \, r^n I_{(2rh-h^2)/r^2} \left(\frac{n+1}{2}, \frac{1}{2} \right) , \)
and the area formula A can be expressed in terms of the area of the unit n-ball \(A_{n}={\scriptstyle 2\pi^{n/2}/\Gamma[\frac{n}{2}]} \) as
\( A =\frac{1}{2}A_{n} \, r^{n-1} I_{(2rh-h^2)/r^2} \left(\frac{n-1}{2}, \frac{1}{2} \right) , \)
where \(\scriptstyle 0\le h\le r . \)
Earlier in [5] (1986, USSR Academ. Press) the formulas were received: \(A=A_n p_ { n-2 } (q), V=V_n p_n (q) \), where \( q= 1-h/r (0 \le q \le 1 ), p_n (q) =(1-G_n(q)/G_n(1))/2, \)
\(G _n(q)= \int \limits_{0}^{q} (1-t^2) ^ { (n-1) /2 } dt. \)
For odd n=2k+1:
\(G_n(q) = \sum_{i=0}^k (-1) ^i \binom k i \frac {q^{2i+1}} {2i+1}. \)
It is shown in [6] that if \(n \to \infty \) and q/n = const., then \( p_n (q) \to 1- F(\sqrt {q/n}) \) where F() is the integral of the standard normal distribution.
See also
Circular segment — the analogous 2D object.
Solid angle — contains formula for n-sphere caps
Spherical segment
Spherical sector
Spherical wedge
References
Connolly, Michael L. (1985). "Computation of molecular volume". J. Am. Chem. Soc: 1118–1124. doi:10.1021/ja00291a006.
Pavani, R.; Ranghino, G. (1982). "A method to compute the volume of a molecule". Comput. Chem. doi:10.1016/0097-8485(82)80006-5.
Bondi, A. (1964). "van der Waals volumes and radii". J. Phys. Chem. (68): 441–451. doi:10.1021/j100785a001.
Li, S. (2011). "Concise Formulas for the Area and Volume of a Hyperspherical Cap". Asian J. Math. Stat. 4 (1): 66–70. doi:10.3923/ajms.2011.66.70
Chudnov A.M. (1986). “On Minimax Signal Generation and Reception Algorithms”, Problems of Information Transmission, 22:4 (1986), 49–54, rus. (Mi ppi958, an: 0624.94005)
Chudnov A.M. (1991). “Game-Theoretical Problems of Synthesis of Signal Generation and Reception Algorithms”, Problems of Information Transmission, 27:3 (1991), 57–65, rus. (Mi ppi570, an:0778.94001)
Richmond, Timothy J. (1984). "Solvent accessible surface area and excluded volume in proteins: Analytical equation for overlapping spheres and implications for the hydrophobic effect". J. Molec. Biol. 178 (1): 63–89. doi:10.1016/0022-2836(84)90231-6.
Lustig, Rolf (1986). "Geometry of four hard fused spheres in an arbitrary spatial configuration". Mol. Phys. 59 (2): 195–207. Bibcode:1986MolPh..59..195L. doi:10.1080/00268978600102011.
Gibson, K. D.; Scheraga, Harold A. (1987). "Volume of the intersection of three spheres of unequal size: a simplified formula". J. Phys. Chem. 91 (15): 4121–4122. doi:10.1021/j100299a035.
Gibson, K. D.; Scheraga, Harold A. (1987). "Exact calculation of the volume and surface area of fused hard-sphere molecules with unequal atomic radii". Mol. Phys. 62 (5): 1247–1265. Bibcode:1987MolPh..62.1247G. doi:10.1080/00268978700102951.
Petitjean, Michel (1994). "On the analytical calculation of van der Waals surfaces and volumes: some numerical aspects". Int. J. Quant. Chem. 15 (5): 507–523. doi:10.1002/jcc.540150504.
Grant, J. A.; Pickup, B. T. (1995). "A Gaussian description of molecular shape". J. Phys. Chem. 99 (11): 3503–3510. doi:10.1021/j100011a016.
Busa, Jan; Dzurina, Jozef; Hayryan, Edik; Hayryan, Shura (2005). "ARVO: A fortran package for computing the solvent accessible surface area and the excluded volume of overlapping spheres via analytic equations". Comp. Phys. Commun. 165: 59–96. Bibcode:2005CoPhC.165...59B. doi:10.1016/j.cpc.2004.08.002.
Li, S. (2011). "Concise Formulas for the Area and Volume of a Hyperspherical Cap". Asian J. Math. Stat. 4 (1): 66–70. doi:10.3923/ajms.2011.66.70..
External links
Weisstein, Eric W., "Spherical cap", MathWorld., derivation and some additional formulas
Online calculator for spherical cap volume and area
Summary of spherical formulas
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

