.

In geometry, a spherical segment is the solid defined by cutting a sphere with a pair of parallel planes.

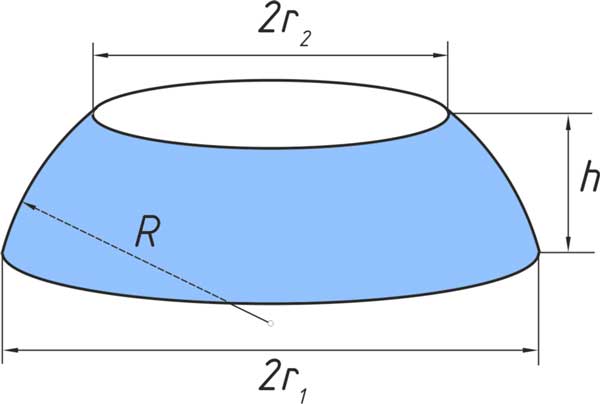
It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum. The surface of the spherical segment (excluding the bases) is called spherical zone.

If the radius of the sphere is called R, the radius of the spherical segment bases \( r_1 \) and \( r_2 \), and the height of the segment (the distance from one parallel plane to the other) called h, the volume of the spherical segment is then:

\( V = \frac {\pi h}{6} (3r_1^2 + 3r_2^2 + h^2) \, \)

The area of the spherical zone —which excludes the top and bottom bases— is given by:

\( A = 2 \pi R h \, \)

.

Spherical segment