.
Ulam spiral
The Ulam spiral, or prime spiral (in other languages also called the Ulam Cloth) is a simple method of visualizing the prime numbers that reveals the apparent tendency of certain quadratic polynomials to generate unusually large numbers of primes. It was discovered by the mathematician Stanislaw Ulam in 1963, while he was doodling during the presentation of a “long and very boring paper”[1] at a scientific meeting. Shortly afterwards, in an early application of computer graphics, Ulam with collaborators Myron Stein and Mark Wells used MANIAC II at Los Alamos Scientific Laboratory to produce pictures of the spiral for numbers up to 65,000.[2][1][3] In March of the following year, Martin Gardner wrote about the Ulam spiral in his Mathematical Games column;[1] the Ulam spiral featured on the front cover of the issue of Scientific American in which the column appeared.
Construction
Ulam constructed the spiral by writing down a regular rectangular grid of numbers, starting with 1 at the center, and spiraling out:

Numbers from 1 to 49 placed in spiral order
He then circled all of the prime numbers and he got the following picture:
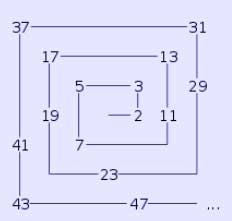
Small Ulam spiral
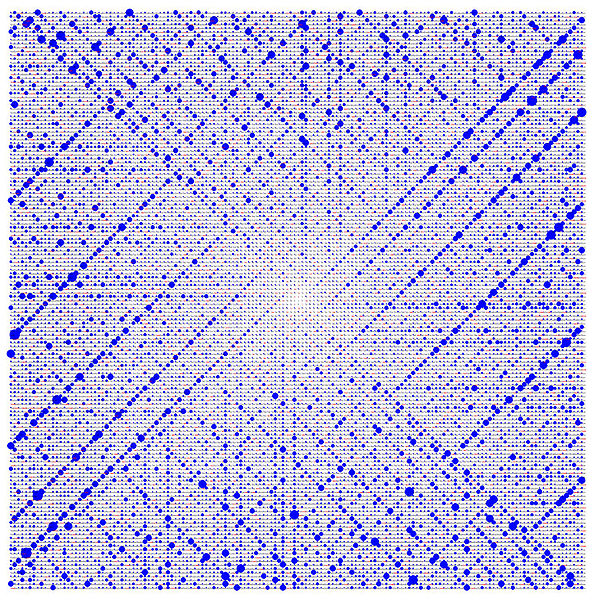
The Ulam spiral to 150 iterations. Red dots represent prime numbers; blue dots represent composite numbers, with the size of the dot indicating the degree of compositeness.
To his surprise, the circled numbers tended to line up along diagonal lines.
All prime numbers, except for the number 2, are odd numbers. Since in the Ulam spiral adjacent diagonals are alternatively odd and even numbers, it is no surprise that all prime numbers lie in alternate diagonals of the Ulam spiral. What is startling is the tendency of prime numbers to lie on some diagonals more than others.
Tests so far confirm that there are diagonal lines even when many numbers are plotted. The pattern also seems to appear even if the number at the center is not 1 (and can, in fact, be much larger than 1). This implies that there are many integer constants b and c such that the function:
\( f(n) = 4 n^2 + b n + c \)
generates, as n counts up {1, 2, 3, ...}, a number of primes that is large by comparison with the proportion of primes among numbers of similar magnitude.
According to Ed Pegg, Jr., the herpetologist Laurence M. Klauber proposed the use of a prime number spiral in finding prime-rich quadratic polynomials in 1932, more than thirty years prior to Ulam's discovery.[4]
Hardy and Littlewood's Conjecture F
In their famous 1923 paper on the Goldbach Conjecture, Hardy and Littlewood stated a series of conjectures, one of which, if true, would explain some of the striking features of the Ulam spiral. This conjecture, which Hardy and Littlewood called “Conjecture F”, is a special case of the Bateman–Horn conjecture and asserts an asymptotic formula for the number of primes of the form ax2+bx+c. Rays emanating from the central region of the Ulam spiral making angles of 45° with the horizontal and vertical correspond to numbers of the form 4x2+bx+c with b even; horizontal and vertical rays correspond to numbers of the same form with b odd. Conjecture F provides a formula that can be used to estimate the density of primes along such rays. It implies that there will be considerable variability in the density along different rays. In particular, the density is highly sensitive to the discriminant of the polynomial, b2−16c.
Conjecture F is concerned with polynomials of the form ax2+bx+c where a, b, and c are integers and a is positive. If the coefficients contain a common factor greater than 1 or if the discriminant Δ=b2−4ac is a perfect square, the polynomial factorizes and therefore produces composite numbers as x takes the values 0, 1, 2, ... (except possibly for one or two values of x where one of the factors equals 1). Moreover, if a+b and c are both even, the polynomial produces only even values, and is therefore composite except possibly for the value 2. Hardy and Littlewood assert that, apart from these situations, ax2+bx+c takes prime values infinitely often as x takes the values 0, 1, 2, ... This statement is a special case of an earlier conjecture of Bunyakovsky and remains open. Hardy and Littlewood further assert that, asymptotically, the number P(n) of primes of the form ax2+bx+c and less than n is given by
\( P(n)\sim A\frac{1}{\sqrt{a}}\frac{\sqrt{n}}{\log n} \)
where A depends on a, b, and c but not on n. By the prime number theorem, this formula with A set equal to one is the asymptotic number of primes less than n expected in a random set of numbers having the same density as the set of numbers of the form ax2+bx+c. But since A can take values bigger or smaller than 1, some polynomials, according to the conjecture, will be especially rich in primes, and others especially poor. An unusually rich polynomial is 4x2−2x+41 which forms a visible line in the Ulam spiral. The constant A for this polynomial is approximately 6.6, meaning that the numbers it generates are almost seven times as likely to be prime as random numbers of comparable size, according to the conjecture. This particular polynomial is related to Euler's prime-generating polynomial x2−x+41 by replacing x with 2x, or equivalently, by restricting x to the even numbers. Hardy and Littlewood's formula for the constant A is
\( A=\varepsilon\prod_p\left(\frac{p}{p-1}\right)\prod_{\varpi}\left(1-\frac{1}{\varpi-1}\left(\frac{\Delta}{\varpi}\right)\right). \)
In the first product, p is a prime dividing both a and b; in the second product, \( \varpi \) is an odd prime not dividing a. The quantity ε is defined to be 1 if a+b is odd and 2 if a+b is even. The symbol \( \left(\frac{\Delta}{\varpi}\right) \) is the Legendre symbol. A quadratic polynomial with A ≈ 11.3, currently the highest known value, has been discovered by Jacobson and Williams.[5][6]
Sacks spiral
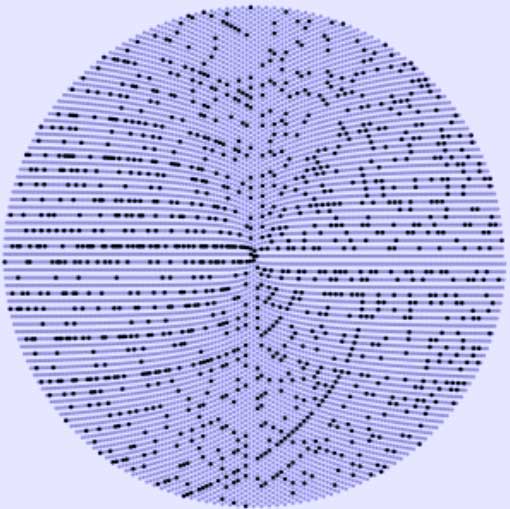
Sacks spiral(*)
Robert Sacks devised a variant of the Ulam spiral in 1994. In the Sacks spiral the non-negative integers are plotted on an Archimedean spiral rather than the square spiral used by Ulam, and are spaced so that one perfect square occurs in each full rotation. (In the Ulam spiral, two squares occur in each rotation.) Euler's prime-generating polynomial, x2−x+41, now appears as a single curve as x takes the values 0, 1, 2, ... This curve asymptotically approaches a horizontal line in the left half of the figure. (In the Ulam spiral, Euler's polynomial forms two diagonal lines, one in the top half of the figure, corresponding to even values of x in the sequence, the other in the bottom half of the figure corresponding to odd values of x in the sequence.)
Notes
^ a b c Gardner 1964, p. 122.
^ Stein, Ulam & Wells 1964, p. 520.
^ Hoffman 1988, p. 41.
^ Pegg, Jr., Ed (July 17, 2006). "Prime generating polynomials". Math Games. Mathematical Association of America. Retrieved 5 July 2010.
^ Jacobson Jr., M. J.; Williams, H. C (2003), "New quadratic polynomials with high densities of prime values", Mathematics of Computation 72 (241): 499–519, doi:10.1090/S0025-5718-02-01418-7
^ Guy, Richard K. (2004), Unsolved problems in number theory (3rd ed.), Springer, p. 8, ISBN 978-0-387-20860-2
References
Gardner, M. (March 1964), "Mathematical Games: The Remarkable Lore of the Prime Number", Scientific American 210: 120–128.
Hardy, G. H.; Littlewood, J. E. (1923), "Some Problems of 'Partitio Numerorum'; III: On the Expression of a Number as a Sum of Primes", Acta Mathematica 44: 1–70, doi:10.1007/BF02403921.
Hoffman, Paul (1988), Archimedes' Revenge: The Joys and Perils of Mathematics, New York: Fawcett Colombine, ISBN 0-449-00089-3.
Stein, M. L.; Ulam, S. M.; Wells, M. B. (1964), "A Visual Display of Some Properties of the Distribution of Primes", American Mathematical Monthly (Mathematical Association of America) 71 (5): 516–520, doi:10.2307/2312588, JSTOR 2312588.
Stein, M.; Ulam, S. M. (1967), "An Observation on the Distribution of Primes", American Mathematical Monthly (Mathematical Association of America) 74 (1): 43–44, doi:10.2307/2314055, JSTOR 2314055.
External links
Video showing the construction of the Ulam Spiral
a 2000 x 2000 Ulam Spiral
a 100000 x 100000 Ulam Spiral (10 Gigapixels)
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

