| == |
A triangular number is the sum of the n natural numbers from 1 to n.
As shown in the rightmost term of this formula, every triangular number is a binomial coefficient: the nth triangular is the number of distinct pairs to be selected from n + 1 objects. The sequence of triangular numbers (sequence A000217 in OEIS) for n = 1, 2, 3... is: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ... Relations to other figurate numbers Triangular numbers have a wide variety of relations to other figurate numbers. Most simply, the sum of two consecutive triangular numbers is a square number. Algebraically,
Alternatively, the same fact can be demonstrated graphically: 16 There are infinitely many triangular numbers that are also square numbers; e.g., 1, 36. Some of them can be generated by a simple recursive formula:
All square triangular numbers are found from the recursion Sn = 34Sn − 1 − Sn − 2 + 2 with S0 = 0 and S1 = 1 Also, the square of the nth triangular number is the same as the sum of the cubes of the integers 1 to n. The sum of the n first triangular numbers is the nth tetrahedral number,
More generally, the difference between the nth m-gonal number and the nth (m + 1)-gonal number is the (n - 1)th triangular number. For example, the sixth heptagonal number (81) minus the sixth hexagonal number (66) equals the fifth triangular number, 15. Every other triangular number is a hexagonal number. Knowing the triangular numbers, one can reckon any centered polygonal number: the nth centered k-gonal number is obtained by the formula Ckn = kTn − 1 + 1 where T is a triangular number. Other properties Every even perfect number is triangular, and no odd perfect numbers are known, hence all known perfect numbers are triangular. In base 10, the digital root of a triangular number is always 1, 3, 6 or 9. Hence every triangular number is either divisible by three or has a remainder of 1 when divided by nine: 6 = 3×2, 10 = 9×1+1, 15 = 3×5, 21 = 3×7, 28 = 9×3+1, ... The inverse of the statement above is, however, not always true. For example, the digital root of 12, which is not a triangular number, is 3 and divisible by three. The sum of the reciprocals of all the triangular numbers is:
This can be shown by using the basic sum of a telescoping series:
Two other interesting formulas regarding triangular numbers are: Ta + b = Ta + Tb + ab and Tab = TaTb + Ta − 1Tb − 1, both of which can easily be established either by looking at dot patterns (see above) or with some simple algebra. In 1796, German mathematician and scientist Carl Friedrich Gauss discovered that every positive integer is representable as a sum of at most three triangular numbers, writing in his diary his famous words, "Heureka! num= Δ + Δ + Δ." Note that this theorem does not imply that the triangular numbers are different (as in the case of 20=10+10), nor that a solution with three nonzero triangular numbers must exist. This is a special case of Fermat's Polygonal Number Theorem. Tests for triangular numbers One can efficiently test whether a positive integer x is a triangular number by computing
If n is an integer, then x is the nth triangular number. If n is not an integer, then x is not triangular. Links * Triangular numbers at cut-the-knot * There exist triangular numbers that are also square at cut-the-knot Retrieved from "http://en.wikipedia.org/" |
|
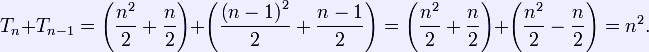 .
. 25
25 
