Cyclide

In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a torus of revolution in Euclidean space. They were discovered by Charles Dupin.

A cyclide is a natural extension of the notion of a quadric surface. Whereas a quadric can be described in terms of second order polynomial in Cartesian coordinates, a cyclide can be obtained by taking such polynomial and adding a term which is proportional to an arbitrary constant times the spherical radius raised to the fourth power:

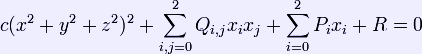
where Q is a 3x3 matrix and P is a 3-dimensional vector and c and R are constants[1].

By definition, the class of cyclides is invariant under Möbius (or conformal) transformations. In fact they are invariant under the larger group of all Lie sphere transformations and form (in some sense) the simplest such class after the spheres. They are therefore particularly significant in Lie sphere geometry[2]. Any Dupin cyclide is a channel surface (i.e., the envelope of a one parameter family of spheres) in two different ways, and in fact this is a characterization. See also Soddy's hexlet.

It has been established in Maxime Bocher's famous dissertation (1891) Ueber die Reihenentwickelungen der Potentialtheorie that the 3 variable Laplace equation can be solved using separation of variables in 17 conformally distinct quadric and cyclidic coordinate geometries. Many other cyclidic geometries can be obtained by studying R-separation of variables in the 3-variable Laplace equation.[3]

Cyclides have the property that the lines of curvature are all circles. Both sheets of the focal surface degenerate to circle.[4]

They were originally defined by Dupin as the envelope of a spheres tangent to three fixed spheres in a continuous manner.

The circular torus is an example of a cyclide.

References

1. ^ Miller, Willard (1977). Symmetry and Separation of Variables.

2. ^ Cecil, Thomas E (1992). Lie sphere geometry. Universitext, Springer-Verlag, New York.

3. ^ Parry Moon; Domina Eberle Spencer (1961). Field Theory Handbook: including coordinate systems, differential equations, and their solutions. Springer. ISBN 0-3870-2732-7.

4. ^ David Hilbert; Cohn-Vossen, S. (1999). Geometry and the Imagination. American Mathematical Society. ISBN 0-8218-1998-4.