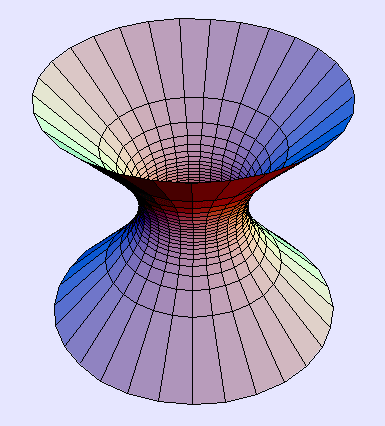
Hyperboloid of one sheet
In mathematics, a hyperboloid is a quadric, a type of surface in three dimensions, described by the equation
![]() (hyperboloid of one sheet),
(hyperboloid of one sheet),
or
![]() (hyperboloid of two sheets).
(hyperboloid of two sheets).
If, and only if, a = b, it is a hyperboloid of revolution. A hyperboloid of revolution of one sheet can be obtained by revolving a hyperbola around its semi-minor axis. Alternatively, a hyperboloid of two sheets of axis AB is obtained as the set of points P such that AP−BP is a constant, AP being the distance between A and P. Points A and B are then called the foci of the hyperboloid. A hyperboloid of revolution of two sheets can be obtained by revolving a hyperbola around its focal axis.
A hyperboloid of one sheet is a doubly ruled surface; if it is a hyperboloid of revolution, it can also be obtained by revolving a line about a skew line.
An elliptic hyperboloid of one sheet. The wires are straight lines. For any point on the surface, there are two straight lines lying entirely on the surface which pass through the point. This illustrates the doubly ruled nature of this surface.
An elliptic hyperboloid of one sheet. The wires are straight lines. For any point on the surface, there are two straight lines lying entirely on the surface which pass through the point. This illustrates the doubly ruled nature of this surface.
A degenerate hyperboloid is of the form
![]()
if a = b then this will give a cone, if not then it gives an elliptical cone.
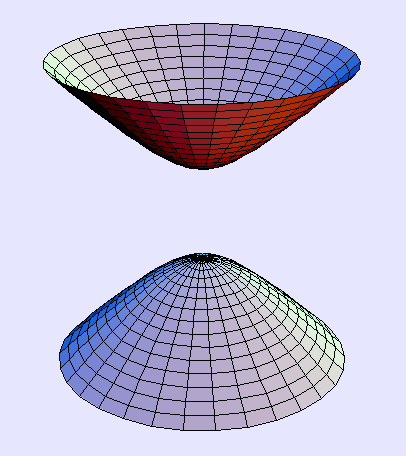
Hyperboloid of two sheets
A notable (and recognizable) use of a hyperboloid structure is in the cooling towers utilized by some power stations. Since a hyperboloid is a doubly-ruled surface, it can be built with straight steel beams, and allows minimisation of wind cross-section while retaining structural integrity with minimal material.
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

