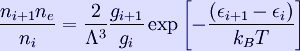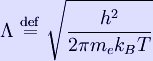|
|
The Saha ionization equation, also known as the Saha-Langmuir equation, was developed by the Indian astrophysicist Megh Nad Saha in 1920, and later (1923) by Irving Langmuir. One of the important applications of the equation was in explaining the spectral classification of stars. The equation is a result of combining ideas of quantum mechanics and statistical mechanics. For a gas at a high enough temperature, the thermal collisions of the atoms will ionize some of the atoms. One or more of the electrons that are normally bound to the atom in orbits around the atomic nucleus will be ejected from the atom and will form an electron gas that co-exists with the gas of atomic ions and neutral atoms. This state of matter is called a plasma. The Saha equation describes the degree of ionization of this plasma as a function of the temperature, density, and ionization energies of the atoms. The Saha equation only holds for weakly ionized plasmas for which the Debye length is large. This means that the "screening" of the coulomb charge of ions and electrons by other ions and electrons is negligible. The subsequent lowering of the ionization potentials and the "cutoff" of the partition function is therefore also negligible. For a gas composed of a single atomic species, the Saha equation is written:
where: * * * * *
* * * * In the case where only one level of ionization is important, we have n1 = ne and defining the total density n as n = n0 + n1, the Saha equation simplifies to:
where ε is the energy of ionization. The Saha equation is useful for determining the ratio of particle densities for two different ionization levels. The most useful form of the Saha equation for this purpose is
where Z denotes the partition function. The Saha equation can be seen as a restatement of the equilibrium condition for the chemical potentials:
This equation simply states that the potential for an atom of ionization state i to ionize is the same as the potential for an electron and an atom of ionization state i+1; the potentials are equal, therefore the system is in equilibrium and no net change of ionization will occur. Links * A detailed derivation from University of Utah Physics Department * Lecture notes from University of Maryland Department of Astronomy * Saha, Megh Nad; On a Physical Theory of Stellar Spectra, Proceedings of the Royal Society of London, Series A, Volume 99, Issue 697 (May 1921), pp. 135–153 * Langmuir, Irving; and Kingdon, Kenneth H.; The Removal of Thorium from the Surface of a Thoriated Tungsten Filament by Positive Ion Bombardment, Physical Review, Vol. 22, No. 2 (August 1923), pp. 148–160 Retrieved from "http://en.wikipedia.org/" 
|
- |
is the density of atoms in the i-th state of ionization, that is with i electrons removed.
is the degeneracy of states for the i-ions
is the energy required to remove i electrons from a neutral atom, creating an i-level ion.
is the electron density
is the thermal de Broglie wavelength of an electron
is the mass of an electron
is the temperature of the gas
is the Boltzmann constant
is Planck's constant
,