Einstein field equations

The Einstein field equations (EFE) or Einstein's equations are a set of ten equations in Einstein's theory of general relativity in which the fundamental force of gravitation is described as a curved spacetime caused by matter and energy.[1] They were first published in 1915.[2].

The EFE collectively form a tensor equation and equate the curvature of spacetime (as expressed using the Einstein tensor) with the energy and momentum within the spacetime (as expressed using the stress-energy tensor).

The EFE are used to determine the curvature of spacetime resulting from the presence of mass and energy. That is, they determine the metric tensor of spacetime for a given arrangement of stress-energy in the spacetime. Because of the relationship between the metric tensor and the Einstein tensor, the EFE become a set of coupled, non-linear differential equations when used in this way.

Mathematical form

The Einstein field equations (EFE) may be written in the form:[1]

.

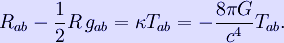where Rab is the Ricci tensor, R the scalar curvature, gab the metric tensor and Tab the stress-energy tensor. The constant κ (kappa) is called the Einstein constant (of gravitation), where π (pi) is Archimedes' constant, G the gravitational constant and c the speed of light.

The above form of the EFE is for the −+++ metric sign convention, which is commonly used in general relativity, and which is used by convention here. Using the +--- metric sign convention leads to an alternate form of the EFE which is

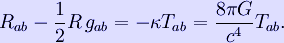
The change of sign on the right hand side occurs because the values of Tab have signs which are determined by the sign convention. On the other hand, the values of the left hand side are convention independent: Rab has values which are independent of the convention because the convention dependencies of R and gab cancel out.

The EFE is a tensor equation relating a set of symmetric 4 x 4 tensors. It is written here using the abstract index notation. Each tensor has 10 independent components. Given the freedom of choice of the four spacetime coordinates, the independent equations reduce to 6 in number.

Although the Einstein field equations were initially formulated in the context of a four-dimensional theory, the equations hold in n dimensions. The equations in contexts outside of general relativity are still referred to as the Einstein field equations (if the dimension is clear).

Despite the simple appearance of the equation it is, in fact, quite complicated. Given a specified distribution of matter and energy in the form of a stress-energy tensor, the EFE are understood to be equations for the metric tensor gab, as both the Ricci tensor and Ricci scalar depend on the metric in a complicated nonlinear manner. In fact, when fully written out, the EFE are a system of 10 coupled, nonlinear, hyperbolic-elliptic partial differential equations.

One can write the EFE in a more compact form by defining the Einstein tensor

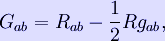
which is a symmetric second-rank tensor that is a function of the metric. The EFE can then be written as

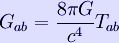
Using geometrized units where G = c = 1, this can be re-written as

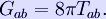
The expression on the left represents the curvature of spacetime as determined by the metric and the expression on the right represents the matter/energy content of spacetime. The EFE can then be interpreted as a set of equations dictating how the curvature of spacetime is related to the matter/energy content of the universe.

These equations, together with the geodesic equation, form the core of the mathematical formulation of general relativity.

Equivalent formulations

Einstein's field equations can be rewritten in the following equivalent "trace-reversed" form

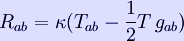
which may be more convenient in some cases (for example, when one is interested in weak-field limit and can replace gμν in the expression on the right with the Minkowski tensor without significant loss of accuracy).

Properties

Conservation of energy and momentum

An important consequence of the EFE is the local conservation of energy and momentum; this result arises by using the differential Bianchi identity to obtain

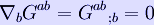
which, by using the EFE, results in

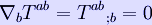
which expresses the local conservation of stress-energy. This conservation law is a physical requirement. With his field equations Einstein automatically satisfied this conservation condition.

Nonlinearity

The nonlinearity of the EFE distinguishes general relativity from many other fundamental physical theories. For example, Maxwell's equations of electromagnetism are linear in the electric and magnetic fields, and charge and current distributions (i.e. the sum of two solutions is also a solution); another example is Schrödinger's equation of quantum mechanics which is linear in the wavefunction.

The correspondence principle

The EFE reduce to Newton's law of gravity by using both the weak-field approximation and the slow-motion approximation. In fact, the constant appearing in the EFE is determined by making these two approximations.

Derivation

The assumptions used in the derivation of Newton's law are as follows:

* The weak-field approximation means that the metric tensor is quasi-Minkowskian, i.e. the metric can be written in diagonal form as,

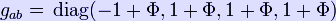
and the stress-energy tensor is assumed to be of the form:

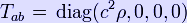
* The slow-motion approximation u < < c implies that the time coordinates are related thus:

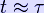
* The Einstein field equations in the trace-reversed form:

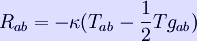
and the geodesic equation:

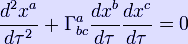
The geodesic equation gives

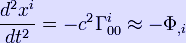
Differentiating this with respect to a spatial coordinate xi gives,

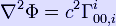
The EFE and the form of the energy-momentum tensor give

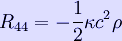
An alternative expression for R₀₀ can be obtained directly from the definition of the Ricci tensor

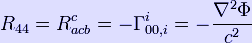
Hence, the two expressions for R00 are equal provided that

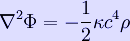
This is Newton's law of gravity in the form of Poisson's equation, provided that :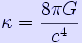

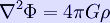
The cosmological constant

One can modify the EFE by introducing a term proportional to the metric:

.

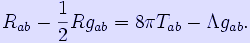The constant Λ is called the cosmological constant. Since Λ is constant, the energy conservation law is unaffected.

The cosmological constant term was originally introduced by Einstein to allow for a static universe (i.e., one that is not expanding or contracting). This effort was unsuccessful for two reasons: the static universe described by this theory was unstable, and observations of distant galaxies by Hubble a decade later confirmed that our universe is, in fact, not static but expanding. So Λ was abandoned, with Einstein calling it the "biggest blunder [he] ever made".[3] For many years the cosmological constant was almost universally considered to be 0.

Despite Einstein's misguided motivation for introducing the cosmological constant term, there is nothing inconsistent with the presence of such a term in the equations. Indeed, recent improved astronomical techniques have found that a non-zero value of Λ is needed to explain some observations.[4][5]

Einstein thought of the cosmological constant as an independent parameter, but its term in the field equation can also be moved algebraically to the other side, written as part of the stress-energy tensor:

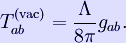
The constant

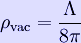
is called the vacuum energy. The existence of a cosmological constant is equivalent to the existence of a non-zero vacuum energy. The terms are now used interchangeably in general relativity.

Solutions

Main article: Solutions of the Einstein field equations

The solutions of the Einstein field equations are metrics of spacetime. The solutions are hence often called 'metrics'. These metrics describe the structure of the spacetime including the inertial motion of objects in the spacetime. As the field equations are non-linear, they cannot always be completely solved (i.e. without making approximations). For example, there is no known complete solution for a spacetime with two massive bodies in it (which is a theoretical model of a binary star system, for example). However, approximations are usually made in these cases. These are commonly referred to as post-Newtonian approximations. Even so, there are numerous cases where the field equations have been solved completely, and those are called exact solutions.[6]

The study of exact solutions of Einstein's field equations is one of the activities of cosmology. It leads to the prediction of black holes and to different models of evolution of the universe.

Vacuum field equations

If the energy-momentum tensor T_μν is zero in the region under consideration, then the field equations are also referred to as the vacuum field equations. By setting T_μν = 0 in the full field equations, the vacuum equations can be written as

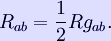
By reversing the trace of this equation, we get the precisely equivalent form

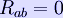
In the case of nonzero cosmological constant, the equations are

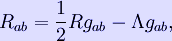
for which the trace-reversed form is

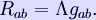
The solutions to the vacuum field equations are called vacuum solutions. Flat Minkowski space is the simplest example of a vacuum solution. Nontrivial examples include the Schwarzschild solution and the Kerr solution.

Manifolds with a vanishing Ricci tensor, Rμν = 0, are referred to as Ricci-flat manifolds and manifolds with a Ricci tensor proportional to the metric as Einstein manifolds.

Einstein-Maxwell equations

If the energy-momentum tensor Tμν is that of an electromagnetic field, i.e. if the electromagnetic stress-energy tensor

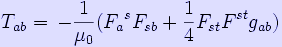
is used, then the Einstein field equations are called the Einstein-Maxwell equations:

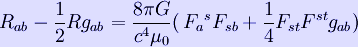
The linearised EFE

Main articles: Linearised Einstein field equations, Linearized gravity

The nonlinearity of the EFE makes finding exact solutions quite difficult. One way of solving the field equations is to make an approximation, namely, that far from the source(s) of gravitating matter, the gravitational field is very weak and the spacetime approximates that of Minkowski space. The metric is then written as the sum of the Minkowski metric and a term representing the deviation of the true metric from the Minkowski metric. This linearisation procedure can be used to discuss the phenomena of gravitational radiation.

See also

* Einstein-Hilbert action

* Exact solutions of Einstein's field equations

* General relativity

* General relativity resources

* History of general relativity

* Mathematics of general relativity

* Solutions of the Einstein field equations

References

See General relativity resources.