Riemannian Penrose inequality

In mathematical general relativity, the Penrose inequality, first conjectured by Sir Roger Penrose, estimates the mass of a spacetime in terms of the total area of its black holes and is a generalization of the positive mass theorem. The Riemannian Penrose inequality is the most important special case. Specifically, if (M, g) is an asymptotically flat Riemannian 3-manifold with nonnegative scalar curvature and ADM mass m, and A is the area of the outermost minimal surface (possibly with multiple connected components), then the Riemannian Penrose inequality asserts

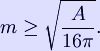
This is purely a geometrical fact, and it corresponds to the case of a complete three-dimensional, space-like, totally geodesic submanifold of a (3 + 1)-dimensional spacetime.

This inequality was first proved by Gerard Huisken and Tom Ilmanen in 1997 in the case where A is the area of the largest outermost minimal surface. Their proof relied on the machinery of inverse mean curvature flow, which they developed. In 1999, Hubert Bray gave the first complete proof of the above inequality using a conformal flow of metrics. Both of the papers were published in 2001.

References

* Bray, H. "Proof of the Riemannian Penrose inequality using the positive mass theorem", Journal of Differential Geometry, 59, (2001) 177-367.

* Huisken, G., and Ilmanen, T. "The inverse mean curvature flow and the Riemannian Penrose inequality", Journal of Differential Geometry, 59, (2001), 353-437.