.

In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces arise as a reaction to external forces applied on the body. Because the loaded deformable body is assumed to behave as a continuum, these internal forces are distributed continuously within the volume of the material body, and result in deformation of the body's shape. Beyond certain limits of material strength, this can lead to a permanent shape change or structural failure.

The stresses considered in continuum mechanics are only those produced during the application of external forces and the consequent deformation of the body, sc. relative changes in deformation are considered rather than absolute values. A body is considered stress-free if the only forces present are those inter-atomic forces (ionic, metallic, and van der Waals forces) required to hold the body together and to keep its shape in the absence of all external influences, including gravitational attraction.[2][3] Stresses generated during manufacture of the body to a specific configuration are also excluded.

The dimension of stress is that of pressure, and therefore the SI unit for stress is the pascal (symbol Pa), which is equivalent to one newton (force) per square meter (unit area), that is N/m2. In Imperial units, stress is measured in pound-force per square inch, which is abbreviated as psi.

Introduction

"Stress" measures the average force per unit area of a surface within a deformable body on which internal forces act, specifically the intensity of the internal forces acting between particles of a deformable body across imaginary internal surfaces.[4] These internal forces are produced between the particles in the body as a reaction to external forces. External forces are either surface forces or body forces. Because the loaded deformable body is assumed to behave as a continuum, these internal forces are distributed continuously within the volume of the material body, i.e. the stress distribution in the body is expressed as a piecewise continuous function of space and time.
Normal stress

For the simple case of an axially loaded body, e.g., a bar subjected to tension or compression by a force passing through its center (Figures 1.2 and 1.3) the stress \( \sigma\,\! \) (sigma), or intensity of internal forces, can be obtained by dividing the total normal force \( F_\mathrm n\,\! \)by the bar's cross-sectional area \( A\,\! \). In the case of a prismatic bar axially loaded, the stress \( \sigma\,\! \) is represented by a scalar called engineering stress or nominal stress that represents an average stress \( (\sigma_\mathrm{avg}\,\!) \) over the area, meaning that the stress in the cross-section is uniformly distributed. Thus, we have

\( \sigma_\mathrm{avg} = \frac{F_\mathrm n}{A}\approx\sigma\,\!. \)

The normal force can be a tensile force if acting outward from the plane, or compressive force if acting inward to the plane.

Normal stress can be caused by several loading methods, the most common being axial tension and compression, bending, and hoop stress. For the case of axial tension or compression (Figure 1.3), the normal stress is observed in two planes \( m-m\,\! \) and \( n-n\,\! \) of the axially loaded prismatic bar. The stress on plane \( n-n\,\!, \) which is closer to the point of application of the load \( F\,\!, \) varies more across the cross-section than that of plane \( m-m\,\! \). However, if the cross-sectional area of the bar is very small, i.e. the bar is slender, the variation of stress across the area is small and the normal stress can be approximated by \( \sigma_\mathrm {avg}\,\! \). On the other hand, the variation of shear stress across the section of a prismatic bar cannot be assumed to be uniform.

In the case of bending of a bar one side is stretched and the other compressed, resulting in axial tensile and compressive normal stresses on the respective sides.

Hoop stress is typically seen in pressure vessels, where internal pressure causes the vessel walls to expand, which results in tensile normal stress.
Shear stress

A different type of stress occurs when the force \( F_\mathrm\,\! \) occurs in shear, as shown in Figure 1.4. \( F_\mathrm s\,\! \) is called the shear force. Dividing the shear force \( F_\mathrm s\,\! \) by the cross-sectional area \( A\,\! \) we obtain the shear stress \( \tau\,\! (tau) \).

\( \tau_\mathrm{avg}= \frac{F_\mathrm s}{A}\approx\tau\,\! \)

Shear stress can also be caused by various loading methods, including direct shear, torsion, and can be significant in bending. A shaft loaded in torsion sees shear stress in the direction tangential to its axis. I-beams see significant shear in the web under bending loads; this is due to the web constraining the flanges.

Combined stresses

Often, mechanical bodies experience more than one type of stress at the same time; this is called combined stress. When two or more stress act on one plane, i.e. bending and shear, this is called biaxial stress. For combined stresses that act in all directions, i.e. bending, torque, and pressure, this is triaxial stress. Various methods for handling combined stresses are included in this article.
Stress modeling (Cauchy)

Stress is generally not uniformly distributed over the cross-section of a material body. Consequently the stress at a given point differs from the average stress over the entire area. Therefore it is necessary to define the stress at a specific point in the body (Figure 1.1). According to Cauchy, the stress at any point in an object, assumed to behave as a continuum, is completely defined by nine component stresses: three orthogonal normal stresses and six orthogonal shear stresses. This can be expressed as a second-order tensor of type (0,2) known as the Cauchy stress tensor. \( \boldsymbol\sigma\,\!: \)

\( \boldsymbol{\sigma}= \left[{\begin{matrix} \sigma _{11} & \sigma _{12} & \sigma _{13} \\ \sigma _{21} & \sigma _{22} & \sigma _{23} \\ \sigma _{31} & \sigma _{32} & \sigma _{33} \\ \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _{xx} & \sigma _{xy} & \sigma _{xz} \\ \sigma _{yx} & \sigma _{yy} & \sigma _{yz} \\ \sigma _{zx} & \sigma _{zy} & \sigma _{zz} \\ \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _x & \tau _{xy} & \tau _{xz} \\ \tau _{yx} & \sigma _y & \tau _{yz} \\ \tau _{zx} & \tau _{zy} & \sigma _z \\ \end{matrix}}\right] \,\! \)

The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle of stress distribution. Certain invariants are associated with the stress tensor, whose values do not depend upon the coordinate system chosen or the area element upon which the stress tensor operates. These are the three eigenvalues of the stress tensor, which are called the principal stresses.

The Cauchy stress tensor is used for stress analysis of material bodies experiencing small deformations where the differences in stress distribution in most cases can be neglected. For large deformations, also called finite deformations, other measures of stress, such as the first and second Piola–Kirchhoff stress tensors, the Biot stress tensor, and the Kirchhoff stress tensor, are required.

According to the principle of conservation of linear momentum, if a continuous body is in static equilibrium it can be demonstrated that the components of the Cauchy stress tensor at every material point in the body satisfy the equilibrium equations (Cauchy’s equations of motion for zero acceleration). At the same time, according to the principle of conservation of angular momentum, equilibrium requires that the summation of moments with respect to an arbitrary point is zero, which leads to the conclusion that the stress tensor is symmetric, thus having only six independent stress components instead of the original nine.

Solids, liquids, and gases have stress fields. Static fluids support normal stress but will flow under shear stress. Moving viscous fluids can support shear stress (dynamic pressure). Solids can support both shear and normal stress, with ductile materials failing under shear and brittle materials failing under normal stress. All materials have temperature dependent variations in stress-related properties, and non-Newtonian materials have rate-dependent variations.
Stress analysis

Stress analysis is the determination of the internal distribution of stresses in a structure. It is needed in engineering for the study and design of structures such as tunnels, dams, mechanical parts, and structural frames, under prescribed or expected loads. To determine the distribution of stress in a structure, the engineer needs to solve a boundary-value problem by specifying the boundary conditions. These are displacements and forces on the boundary of the structure.

Constitutive equations, such as Hooke’s law for linear elastic materials, describe the stress-strain relationship in these calculations.

When a structure is expected to deform elastically (and resume its original shape), a boundary-value problem based on the theory of elasticity is applied, with infinitesimal strains, under design loads.

When the applied loads permanently deform the structure, the theory of plasticity applies.

Stress analysis is simplified when the physical dimensions and the distribution of loads allow the structure to be treated as one- or two-dimensional. For a two-dimensional analysis a plane stress or a plane strain condition can be assumed. Alternatively, stresses can be experimentally determined.

Computer-based approximations for boundary-value problems can be obtained through numerical methods such as the finite element method, the finite difference method, and the boundary element method. Analytical or closed-form solutions can be obtained for simple geometries, constitutive relations, and boundary conditions.
Theoretical background

Continuum mechanics deals with deformable bodies, as opposed to rigid bodies. The stresses considered in continuum mechanics are only those produced during the application of external forces and the consequent deformation of the body, sc. relative changes in deformation are considered rather than absolute values. A body is considered stress-free if the only forces present are those inter-atomic forces (ionic, metallic, and van der Waals forces) required to hold the body together and to keep its shape in the absence of all external influences, including gravitational attraction.[2][3] Stresses generated during manufacture of the body to a specific configuration are also excluded.

Following classical Newtonian and Eulerian dynamics, the motion of a material body is produced by the action of externally applied forces which are assumed to be of two kinds: surface forces and body forces.[5]

Surface forces, or contact forces, can act either on the bounding surface of the body, as a result of mechanical contact with other bodies, or on imaginary internal surfaces that bind portions of the body, as a result of the mechanical interaction between the parts of the body to either side of the surface (#Euler–Cauchy's stress principle). When external contact forces act on a body, internal contact forces pass from point to point inside the body to balance their action, according to Newton's second law of motion of conservation of linear momentum and angular momentum. These laws are called Euler's equations of motion for continuous bodies. The internal contact forces are related to the body's deformation through constitutive equations. This article provides mathematical descriptions of internal contact forces and how they relate to the body's motion, independent of the body's material makeup.[6]

Stress can be thought as a measure of the internal contact forces' intensity acting between particles of the body across imaginary internal surfaces.[4] In other words, stress is a measure of the average quantity of force exerted per unit area of the surface on which these internal forces act. The intensity of contact forces is in inverse proportion to the contact area. For example, if a force applied to a small area is compared to a distributed load of the same resultant magnitude applied to a larger area, one finds that the effects or intensities of these two forces are locally different because the stresses are not the same.

Body forces originate from sources outside of the body[7] that act on its volume (or mass). This implies that the internal forces manifest through the contact forces alone.[8] These forces arise from the presence of the body in force fields, (e.g., a gravitational field). As the mass of a continuous body is assumed to be continuously distributed, any force originating from the mass is also continuously distributed. Thus, body forces are assumed to be continuous over the body's volume.[9]

The density of internal forces at every point in a deformable body is not necessarily even, i.e. there is a distribution of stresses. This variation of internal forces is governed by the laws of conservation of linear and angular momentum, which normally apply to a mass particle but extend in continuum mechanics to a body of continuously distributed mass. If a body is represented as an assemblage of discrete particles, each governed by Newton’s laws of motion, then Euler’s equations can be derived from Newton’s laws. Euler’s equations can, however, be taken as axioms describing the laws of motion for extended bodies, independently of any particle structure.[10]
Euler–Cauchy stress principle

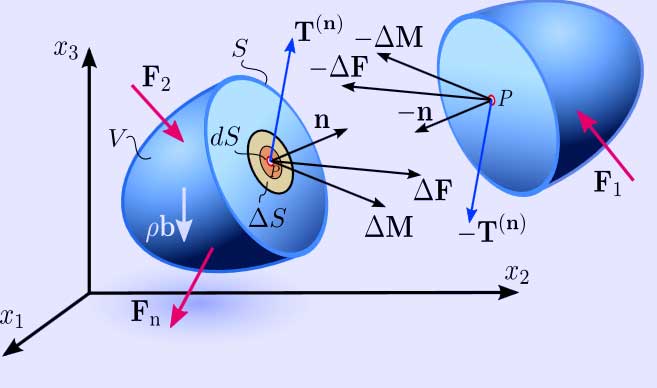
Figure 2.1a (*) Internal distribution of contact forces and couple stresses on a differential \( dS\,\! \)of the internal surface \( S\,\! \) in a continuum, as a result of the interaction between the two portions of the continuum separated by the surface

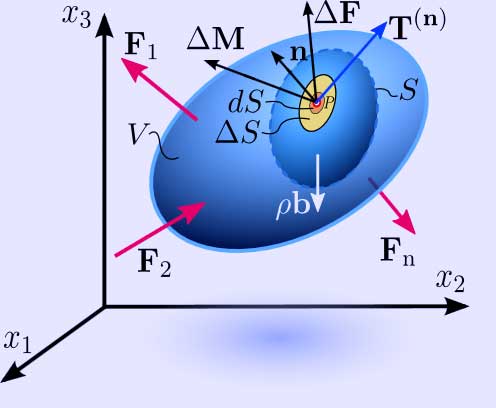
Figure 2.1b (*) Internal distribution of contact forces and couple stresses on a differential \( dS\,\! \) of the internal surface \( S\,\! \) in a continuum, as a result of the interaction between the two portions of the continuum separated by the surface

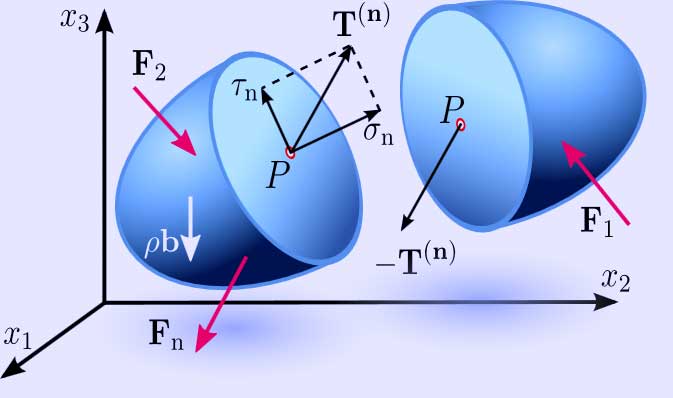
Figure 2.1c (*) Stress vector on an internal surface S with normal vector n. Depending on the orientation of the plane under consideration, the stress vector may not necessarily be perpendicular to that plane, i.e. parallel to \( \mathbf{n}\,\! \), and can be resolved into two components: one component normal to the plane, called normal stress \( \sigma_\mathrm{n} \,\!, \) and another component parallel to this plane, called the shearing stress \( \tau \,\!. \)

The Euler–Cauchy stress principle states that upon any surface (real or imaginary) that divides the body, the action of one part of the body on the other is equivalent (equipollent) to the system of distributed forces and couples on the surface dividing the body,[11] and it is represented by a vector field T(n), called the stress vector, defined on the surface S and assumed to depend continuously on the surface's unit vector n.[9][12]

To explain this principle, consider an imaginary surface S passing through an internal material point P dividing the continuous body into two segments, as seen in Figure 2.1a or 2.1b (some authors use the cutting plane diagram[citation needed] and others use the diagram with the arbitrary volume inside the continuum enclosed by the surface S). The body is subjected to external surface forces F and body forces b. The internal contact forces transmitted from one segment to the other through the dividing plane, due to the action of one portion of the continuum onto the other, generate a force distribution on a small area ΔS, with a normal unit vector n, on the dividing plane S. The force distribution is equipollent to a contact force ΔF and a couple stress ΔM, as shown in Figure 2.1a and 2.1b. Cauchy’s stress principle asserts[2] that as ΔS becomes very small and tends to zero the ratio ΔF/ΔS becomes dF/dS and the couple stress vector ΔM vanishes. In specific fields of continuum mechanics the couple stress is assumed not to vanish; however, classical branches of continuum mechanics address non-polar materials which do not consider couple stresses and body moments. The resultant vector dF/dS is defined as the stress vector or traction vector given by T(n) = Ti(n) ei at the point P associated with a plane with a normal vector n:

\( T^{(\mathbf{n})}_i= \lim_{\Delta S \to 0} \frac {\Delta F_i}{\Delta S} = {dF_i \over dS}. \)

This equation means that the stress vector depends on its location in the body and the orientation of the plane on which it is acting.

Depending on the orientation of the plane under consideration, the stress vector may not necessarily be perpendicular to that plane, i.e. parallel to n, and can be resolved into two components (Figure 2.1c):

one normal to the plane, called normal stress

\( \mathbf{\sigma_\mathrm{n}}= \lim_{\Delta S \to 0} \frac {\Delta F_\mathrm n}{\Delta S} = \frac{dF_\mathrm n}{dS}, \)

where dFn is the normal component of the force dF to the differential area dS

and the other parallel to this plane, called the shear stress

\( \mathbf \tau= \lim_{\Delta S \to 0} \frac {\Delta F_\mathrm s}{\Delta S} = \frac{dF_\mathrm s}{dS}, \)

where dFs is the tangential component of the force dF to the differential surface area dS. The shear stress can be further decomposed into two mutually perpendicular vectors.

Cauchy’s postulate

According to the Cauchy Postulate, the stress vector T(n) remains unchanged for all surfaces passing through the point P and having the same normal vector n at P,[8][13] i.e., having a common tangent at P. This means that the stress vector is a function of the normal vector n only, and is not influenced by the curvature of the internal surfaces.
Cauchy’s fundamental lemma

A consequence of Cauchy’s postulate is Cauchy’s Fundamental Lemma,[3][7][8] also called the Cauchy reciprocal theorem,[14] which states that the stress vectors acting on opposite sides of the same surface are equal in magnitude and opposite in direction. Cauchy’s fundamental lemma is equivalent to Newton's third law of motion of action and reaction, and is expressed as

\( - \mathbf{T}^{(\mathbf{n})}= \mathbf{T}^{(- \mathbf{n})}.\,\! \)

Cauchy’s stress theorem—stress tensor

The state of stress at a point in the body is then defined by all the stress vectors T(n) associated with all planes (infinite in number) that pass through that point.[4] However, according to Cauchy’s fundamental theorem,[3] also called Cauchy’s stress theorem,[7] merely by knowing the stress vectors on three mutually perpendicular planes, the stress vector on any other plane passing through that point can be found through coordinate transformation equations.

Cauchy’s stress theorem states that there exists a second-order tensor field σ(x, t), called the Cauchy stress tensor, independent of n, such that T is a linear function of n:

\( \mathbf{T}^{(\mathbf n)}= \boldsymbol{\sigma}\cdot\mathbf n \quad \text{or} \quad T_j^{(n)}= \sigma_{ij}n_i.\,\! \)

This equation implies that the stress vector T(n) at any point P in a continuum associated with a plane with normal unit vector n can be expressed as a function of the stress vectors on the planes perpendicular to the coordinate axes, i.e. in terms of the components σij of the stress tensor σ.

To prove this expression, consider a tetrahedron with three faces oriented in the coordinate planes, and with an infinitesimal area dA oriented in an arbitrary direction specified by a normal unit vector n (Figure 2.2). The tetrahedron is formed by slicing the infinitesimal element along an arbitrary plane n. The stress vector on this plane is denoted by T(n). The stress vectors acting on the faces of the tetrahedron are denoted as T(e1), T(e2), and T(e3), and are by definition the components σij of the stress tensor σ. This tetrahedron is sometimes called the Cauchy tetrahedron. The equilibrium of forces, i.e. Euler’s first law of motion (Newton’s second law of motion), gives:

\( \mathbf{T}^{(\mathbf{n})} \, dA - \mathbf{T}^{(\mathbf{e}_1)} \, dA_1 - \mathbf{T}^{(\mathbf{e}_2)} \, dA_2 - \mathbf{T}^{(\mathbf{e}_3)} \, dA_3 = \rho \left( \frac{h}{3}dA \right) \mathbf{a},\,\! \)

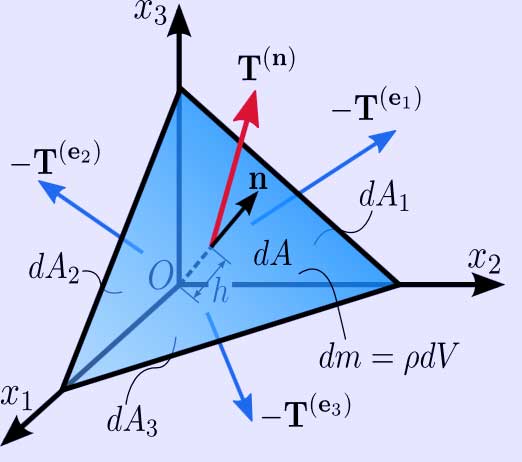
Figure 2.2 (*). Stress vector acting on a plane with normal unit vector n.
A note on the sign convention: The tetrahedron is formed by slicing a parallelepiped along an arbitrary plane n. So, the force acting on the plane n is the reaction exerted by the other half of the parallelepiped and has an opposite sign.

where the right-hand-side represents the product of the mass enclosed by the tetrahedron and its acceleration: ρ is the density, a is the acceleration, and h is the height of the tetrahedron, considering the plane n as the base. The area of the faces of the tetrahedron perpendicular to the axes can be found by projecting dA into each face (using the dot product):

\( dA_1= \left(\mathbf{n} \cdot \mathbf{e}_1 \right)dA = n_1 \; dA,\,\! \)
\( dA_2= \left(\mathbf{n} \cdot \mathbf{e}_2 \right)dA = n_2 \; dA,\,\! \)
\( dA_3= \left(\mathbf{n} \cdot \mathbf{e}_3 \right)dA = n_3 \; dA,\,\! \)

and then substituting into the equation to cancel out dA:

\( \mathbf{T}^{(\mathbf{n})} - \mathbf{T}^{(\mathbf{e}_1)}n_1 - \mathbf{T}^{(\mathbf{e}_2)}n_2 - \mathbf{T}^{(\mathbf{e}_3)}n_3 = \rho \left( \frac{h}{3} \right) \mathbf{a}.\,\! \)

To consider the limiting case as the tetrahedron shrinks to a point, h must go to 0 (intuitively, the plane n is translated along n toward O). As a result, the right-hand-side of the equation approaches 0, so

\( \mathbf{T}^{(\mathbf{n})} = \mathbf{T}^{(\mathbf{e}_1)} n_1 + \mathbf{T}^{(\mathbf{e}_2)} n_2 + \mathbf{T}^{(\mathbf{e}_3)} n_3.\,\! \)

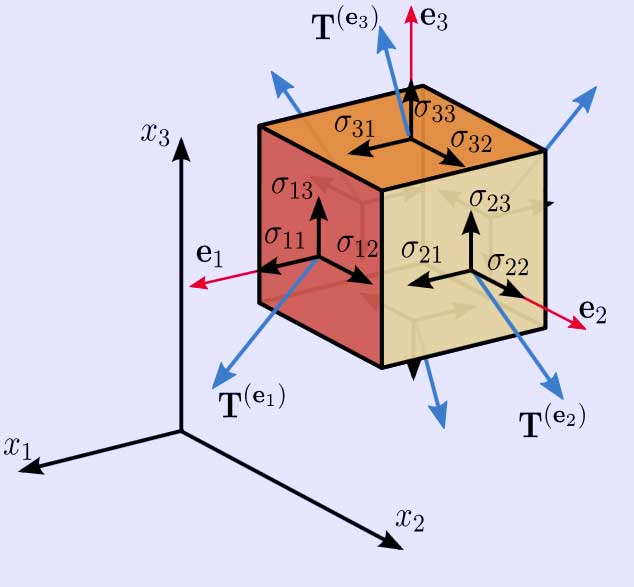
Figure 2.3 (*) Components of stress in three dimensions

Assuming a material element (Figure 2.3) with planes perpendicular to the coordinate axes of a Cartesian coordinate system, the stress vectors associated with each of the element planes, i.e. T(e1), T(e2), and T(e3) can be decomposed into a normal component and two shear components, i.e. components in the direction of the three coordinate axes. For the particular case of a surface with normal unit vector oriented in the direction of the x1-axis, denote the normal stress by σ11, and the two shear stresses as σ12 and σ13:

\( \mathbf{T}^{(\mathbf{e}_1)}= T_1^{(\mathbf{e}_1)}\mathbf{e}_1 + T_2^{(\mathbf{e}_1)} \mathbf{e}_2 + T_3^{(\mathbf{e}_1)} \mathbf{e}_3 = \sigma_{11} \mathbf{e}_1 + \sigma_{12} \mathbf{e}_2 + \sigma_{13} \mathbf{e}_3, \)
\( \mathbf{T}^{(\mathbf{e}_2)}= T_1^{(\mathbf{e}_2)}\mathbf{e}_1 + T_2^{(\mathbf{e}_2)} \mathbf{e}_2 + T_3^{(\mathbf{e}_2)} \mathbf{e}_3=\sigma_{21} \mathbf{e}_1 + \sigma_{22} \mathbf{e}_2 + \sigma_{23} \mathbf{e}_3, \)
\( \mathbf{T}^{(\mathbf{e}_3)}= T_1^{(\mathbf{e}_3)}\mathbf{e}_1 + T_2^{(\mathbf{e}_3)} \mathbf{e}_2 + T_3^{(\mathbf{e}_3)} \mathbf{e}_3=\sigma_{31} \mathbf{e}_1 + \sigma_{32} \mathbf{e}_2 + \sigma_{33} \mathbf{e}_3, \)

In index notation this is

\( \mathbf{T}^{(\mathbf{e}_i)}= T_j^{(\mathbf{e}_i)} \mathbf{e}_j = \sigma_{ij} \mathbf{e}_j. \)

The nine components σij of the stress vectors are the components of a second-order Cartesian tensor called the Cauchy stress tensor, which completely defines the state of stress at a point and is given by

\( \boldsymbol{\sigma}= \sigma_{ij} = \left[{\begin{matrix} \mathbf{T}^{(\mathbf{e}_1)} \\ \mathbf{T}^{(\mathbf{e}_2)} \\ \mathbf{T}^{(\mathbf{e}_3)} \\ \end{matrix}}\right] = \left[{\begin{matrix} \sigma _{11} & \sigma _{12} & \sigma _{13} \\ \sigma _{21} & \sigma _{22} & \sigma _{23} \\ \sigma _{31} & \sigma _{32} & \sigma _{33} \\ \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _{xx} & \sigma _{xy} & \sigma _{xz} \\ \sigma _{yx} & \sigma _{yy} & \sigma _{yz} \\ \sigma _{zx} & \sigma _{zy} & \sigma _{zz} \\ \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _x & \tau _{xy} & \tau _{xz} \\ \tau _{yx} & \sigma _y & \tau _{yz} \\ \tau _{zx} & \tau _{zy} & \sigma _z \\ \end{matrix}}\right], \)

where σ₁₁, σ₂₂, and σ₃₃ are normal stresses, and σ₁₂, σ₁₃, σ₂₁, σ₂₃, σ₃₁, and σ₃₂ are shear stresses. The first index i indicates that the stress acts on a plane normal to the x_i-axis, and the second index j denotes the direction in which the stress acts. A stress component is positive if it acts in the positive direction of the coordinate axes, and if the plane where it acts has an outward normal vector pointing in the positive coordinate direction.

Thus, using the components of the stress tensor

\( \begin{align} \mathbf{T}^{(\mathbf{n})} &= \mathbf{T}^{(\mathbf{e}_1)}n_1 + \mathbf{T}^{(\mathbf{e}_2)}n_2 + \mathbf{T}^{(\mathbf{e}_3)}n_3 \\ & = \sum_{i=1}^3 \mathbf{T}^{(\mathbf{e}_i)}n_i \\ &= \left( \sigma_{ij}\mathbf{e}_j \right)n_i \\ &= \sigma_{ij}n_i\mathbf{e}_j \end{align} \)

or, equivalently,

\( T_j^{(\mathbf n)}= \sigma_{ij}n_i. \)

Alternatively, in matrix form we have

\( \left[{\begin{matrix} T^{(\mathbf n)}_1 & T^{(\mathbf n)}_2 & T^{(\mathbf n)}_3\end{matrix}}\right]=\left[{\begin{matrix} n_1 & n_2 & n_3 \end{matrix}}\right]\cdot \left[{\begin{matrix} \sigma _{11} & \sigma _{12} & \sigma _{13} \\ \sigma _{21} & \sigma _{22} & \sigma _{23} \\ \sigma _{31} & \sigma _{32} & \sigma _{33} \\ \end{matrix}}\right]. \)

The Voigt notation representation of the Cauchy stress tensor takes advantage of the symmetry of the stress tensor to express the stress as a six-dimensional vector of the form:

\( \boldsymbol{\sigma} = \begin{bmatrix}\sigma_1 & \sigma_2 & \sigma_3 & \sigma_4 & \sigma_5 & \sigma_6 \end{bmatrix}^T \equiv \begin{bmatrix}\sigma_{11} & \sigma_{22} & \sigma_{33} & \sigma_{23} & \sigma_{31} & \sigma_{12} \end{bmatrix}^T.\,\! \)

The Voigt notation is used extensively in representing stress-strain relations in solid mechanics and for computational efficiency in numerical structural mechanics software.
Transformation rule of the stress tensor

It can be shown that the stress tensor is a contravariant second order tensor, which is a statement of how it transforms under a change of the coordinate system. From an xi -system to an xi'-system, the components σij in the initial system are transformed into the components σij' in the new system according to the tensor transformation rule (Figure 2.4):

\( \sigma^'_{ij}=a_{im}a_{jn}\sigma_{mn} \quad \text{or} \quad \boldsymbol{\sigma}' = \mathbf A \boldsymbol{\sigma} \mathbf A^T, \)

where A is a rotation matrix with components aij. In matrix form this is

\( \left[{\begin{matrix} \sigma^'_{11} & \sigma^'_{12} & \sigma^'_{13} \\ \sigma^'_{21} & \sigma^'_{22} & \sigma^'_{23} \\ \sigma^'_{31} & \sigma^'_{32} & \sigma^'_{33} \\ \end{matrix}}\right]=\left[{\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{matrix}}\right]\left[{\begin{matrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \\ \end{matrix}}\right]\left[{\begin{matrix} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \\ \end{matrix}}\right]. \)

Figure 2.4 Transformation of the stress tensor

Expanding the matrix operation, and simplifying terms using the symmetry of the stress tensor, gives

\( \sigma_{11}' = a_{11}^2\sigma_{11}+a_{12}^2\sigma_{22}+a_{13}^2\sigma_{33}+2a_{11}a_{12}\sigma_{12}+2a_{11}a_{13}\sigma_{13}+2a_{12}a_{13}\sigma_{23}, \)

\( \sigma_{11}' = a_{11}^2\sigma_{11}+a_{12}^2\sigma_{22}+a_{13}^2\sigma_{33}+2a_{11}a_{12}\sigma_{12}+2a_{11}a_{13}\sigma_{13}+2a_{12}a_{13}\sigma_{23}, \)
\( \sigma_{22}' = a_{21}^2\sigma_{11}+a_{22}^2\sigma_{22}+a_{23}^2\sigma_{33}+2a_{21}a_{22}\sigma_{12}+2a_{21}a_{23}\sigma_{13}+2a_{22}a_{23}\sigma_{23}, \)
\( \sigma_{33}' = a_{31}^2\sigma_{11}+a_{32}^2\sigma_{22}+a_{33}^2\sigma_{33}+2a_{31}a_{32}\sigma_{12}+2a_{31}a_{33}\sigma_{13}+2a_{32}a_{33}\sigma_{23}, \)
\( \begin{align} \sigma_{12}' = &a_{11}a_{21}\sigma_{11}+a_{12}a_{22}\sigma_{22}+a_{13}a_{23}\sigma_{33}\\ &+(a_{11}a_{22}+a_{12}a_{21})\sigma_{12}+(a_{12}a_{23}+a_{13}a_{22})\sigma_{23}+(a_{11}a_{23}+a_{13}a_{21})\sigma_{13}, \end{align} \)
\( \begin{align} \sigma_{23}' = &a_{21}a_{31}\sigma_{11}+a_{22}a_{32}\sigma_{22}+a_{23}a_{33}\sigma_{33}\\ &+(a_{21}a_{32}+a_{22}a_{31})\sigma_{12}+(a_{22}a_{33}+a_{23}a_{32})\sigma_{23}+(a_{21}a_{33}+a_{23}a_{31})\sigma_{13},\end{align} \)
\( \begin{align} \sigma_{13}' = &a_{11}a_{31}\sigma_{11}+a_{12}a_{32}\sigma_{22}+a_{13}a_{33}\sigma_{33}\\ &+(a_{11}a_{32}+a_{12}a_{31})\sigma_{12}+(a_{12}a_{33}+a_{13}a_{32})\sigma_{23}+(a_{11}a_{33}+a_{13}a_{31})\sigma_{13}.\end{align} \)

The Mohr circle for stress is a graphical representation of this transformation of stresses.
Normal and shear stresses

The magnitude of the normal stress component σn of any stress vector T(n) acting on an arbitrary plane with normal vector n at a given point, in terms of the components σij of the stress tensor σ, is the dot product of the stress vector and the normal vector:

\( \begin{align} \sigma_\mathrm{n} &= \mathbf{T}^{(\mathbf{n})}\cdot \mathbf{n} \\ &=T^{(\mathbf n)}_i n_i \\ &=\sigma_{ij}n_i n_j. \end{align} \)

The magnitude of the shear stress component τn, acting in the plane spanned by the two vectors T(n) and n, can then be found using the Pythagorean theorem:

\( \begin{align} \tau_\mathrm{n} &=\sqrt{ \left( T^{(\mathbf n)} \right)^2-\sigma_\mathrm{n}^2} \\ &= \sqrt{T_i^{(\mathbf n)}T_i^{(\mathbf n)}-\sigma_\mathrm{n}^2}, \end{align} \)

where

\( \left( T^{(\mathbf n)} \right)^2 = T_i^{(\mathbf n)} T_i^{(\mathbf n)} = \left( \sigma_{ij} n_j \right) \left(\sigma_{ik} n_k \right) = \sigma_{ij} \sigma_{ik} n_j n_k. \)

Equilibrium equations and symmetry of the stress tensor
Figure 4. Continuum body in equilibrium

When a body is in equilibrium the components of the stress tensor in every point of the body satisfy the equilibrium equations,

\( \sigma_{ji,j}+ F_i = 0 \,\! \)

For example, for a hydrostatic fluid in equilibrium conditions, the stress tensor takes on the form:

\( {\sigma_{ij}} = -p{\delta_{ij}}\ , \)

where p is the hydrostatic pressure, and \( {\delta_{ij}}\ \) is the kronecker delta.

Derivation of equilibrium equations

At the same time, equilibrium requires that the summation of moments with respect to an arbitrary point is zero, which leads to the conclusion that the stress tensor is symmetric, i.e.

\( \sigma_{ij}=\sigma_{ji}\,\! \)

Derivation of symmetry of the stress tensor

However, in the presence of couple-stresses, i.e. moments per unit volume, the stress tensor is non-symmetric. This also is the case when the Knudsen number is close to one, \( K_{n}\rightarrow 1\,\!, \) or the continuum is a non-Newtonian fluid, which can lead to rotationally non-invariant fluids, such as polymers.
Principal stresses and stress invariants

At every point in a stressed body there are at least three planes, called principal planes, with normal vectors \( \mathbf{n}\,\! \), called principal directions, where the corresponding stress vector is perpendicular to the plane, i.e., parallel or in the same direction as the normal vector \( \mathbf{n}\,\!, \) and where there are no normal shear stresses \( \tau_\mathrm{n}\,\!. \) The three stresses normal to these principal planes are called principal stresses.

The components \( \sigma_{ij}\,\! \) of the stress tensor depend on the orientation of the coordinate system at the point under consideration. However, the stress tensor itself is a physical quantity and as such, it is independent of the coordinate system chosen to represent it. There are certain invariants associated with every tensor which are also independent of the coordinate system. For example, a vector is a simple tensor of rank one. In three dimensions, it has three components. The value of these components will depend on the coordinate system chosen to represent the vector, but the length of the vector is a physical quantity (a scalar) and is independent of the coordinate system chosen to represent the vector. Similarly, every second rank tensor (such as the stress and the strain tensors) has three independent invariant quantities associated with it. One set of such invariants are the principal stresses of the stress tensor, which are just the eigenvalues of the stress tensor. Their direction vectors are the principal directions or eigenvectors.

A stress vector parallel to the normal vector \( \mathbf{n}\,\! \) is given by:

\( \mathbf{T}^{(\mathbf{n})} = \lambda \mathbf{n}= \mathbf{\sigma}_\mathrm n \mathbf{n}\,\! \)

where \( \lambda\,\! \) is a constant of proportionality, and in this particular case corresponds to the magnitudes \( \sigma_\mathrm{n}\,\! \) of the normal stress vectors or principal stresses.

Knowing that \( T_i^{(n)}=\sigma_{ij}n_j\,\! \) and \( n_i=\delta_{ij}n_j\,\!, \) we have

\( \begin{align} T_i^{(n)} &= \lambda n_i \\ \sigma_{ij}n_j &=\lambda n_i \\ \sigma_{ij}n_j -\lambda n_i &=0 \\ \left(\sigma_{ij}- \lambda\delta_{ij} \right)n_j &=0 \\ \end{align}\,\! \)

This is a homogeneous system, i.e. equal to zero, of three linear equations where \( n_j\,\! \) are the unknowns. To obtain a nontrivial (non-zero) solution for \( n_j\,\!, \) the determinant matrix of the coefficients must be equal to zero, i.e. the system is singular. Thus,

\( \left|\sigma_{ij}- \lambda\delta_{ij} \right|=\begin{vmatrix} \sigma_{11} - \lambda & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} - \lambda & \sigma_{23} \\ \sigma_{31}& \sigma_{32} & \sigma_{33} - \lambda \\ \end{vmatrix}=0\,\! \)

Expanding the determinant leads to the characteristic equation

\( \left|\sigma_{ij}- \lambda\delta_{ij} \right| = -\lambda^3 + I_1\lambda^2 - I_2\lambda + I_3=0\,\! \)

where

\( \begin{align} I_1 &= \sigma_{11}+\sigma_{22}+\sigma_{33} \\ &= \sigma_{kk} \\ I_2 &= \begin{vmatrix} \sigma_{22} & \sigma_{23} \\ \sigma_{32} & \sigma_{33} \\ \end{vmatrix} + \begin{vmatrix} \sigma_{11} & \sigma_{13} \\ \sigma_{31} & \sigma_{33} \\ \end{vmatrix} + \begin{vmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \\ \end{vmatrix} \\ &= \sigma_{11}\sigma_{22}+\sigma_{22}\sigma_{33}+\sigma_{11}\sigma_{33}-\sigma_{12}^2-\sigma_{23}^2-\sigma_{31}^2 \\ &= \frac{1}{2}\left(\sigma_{ii}\sigma_{jj}-\sigma_{ij}\sigma_{ji}\right) \\ I_3 &= \det(\sigma_{ij}) \\ &= \sigma_{11}\sigma_{22}\sigma_{33}+2\sigma_{12}\sigma_{23}\sigma_{31}-\sigma_{12}^2\sigma_{33}-\sigma_{23}^2\sigma_{11}-\sigma_{31}^2\sigma_{22} \\ \end{align} \,\! \)

The characteristic equation has three real roots \( \lambda_i\,\!, \) i.e. not imaginary due to the symmetry of the stress tensor. The \( \sigma_1 = max \left( \lambda_1,\lambda_2,\lambda_3 \right)\,\!, \sigma_3 = min \left( \lambda_1,\lambda_2,\lambda_3 \right)\,\! \) and \( \sigma_2=I_1-\sigma_1-\sigma_3\,\!, \) are the principal stresses, functions of the eigenvalues \( \lambda_i\,\!. \) The eigenvalues are the roots of the Cayley–Hamilton theorem. The principal stresses are unique for a given stress tensor. Therefore, from the characteristic equation, the coefficients \( I_1\,\!, I_2\,\! \) and \( I_3\,\! \), called the first, second, and third stress invariants, respectively, have always the same value regardless of the coordinate system's orientation.

For each eigenvalue, there is a non-trivial solution for \( n_j\,\! \) in the equation \( \left(\sigma_{ij}- \lambda\delta_{ij} \right)n_j =0\,\!. \) These solutions are the principal directions or eigenvectors defining the plane where the principal stresses act. The principal stresses and principal directions characterize the stress at a point and are independent of the orientation.

A coordinate system with axes oriented to the principal directions implies that the normal stresses are the principal stresses and the stress tensor is represented by a diagonal matrix:

\( \sigma_{ij}= \begin{bmatrix} \sigma_1 & 0 & 0\\ 0 & \sigma_2 & 0\\ 0 & 0 & \sigma_3 \end{bmatrix} \,\! \)

The principal stresses can be combined to form the stress invariants, \( I_1\,\!, I_2\,\!, \) and \( I_3\,\!. \) The first and third invariant are the trace and determinant respectively, of the stress tensor. Thus,

\( \begin{align} I_1 &= \sigma_{1}+\sigma_{2}+\sigma_{3} \\ I_2 &= \sigma_{1}\sigma_{2}+\sigma_{2}\sigma_{3}+\sigma_{3}\sigma_{1} \\ I_3 &= \sigma_{1}\sigma_{2}\sigma_{3} \\ \end{align}\,\! \)

Because of its simplicity, the principal coordinate system is often useful when considering the state of the elastic medium at a particular point. Principal stresses are often expressed in the following equation for evaluating stresses in the x and y directions or axial and bending stresses on a part.[15] The principal normal stresses can then be used to calculate the von Mises stress and ultimately the safety factor and margin of safety.

\( \sigma_{1},\sigma_{2}= \frac{\sigma_{x} + \sigma_{y}}{2} \pm \sqrt{\left (\frac{\sigma_{x} - \sigma_{y}}{2}\right)^2 + \tau_{xy}^2}\,\! \)

Using just the part of the equation under the square root is equal to the maximum and minimum shear stress for plus and minus. This is shown as:

\( \tau_{max},\tau_{min}= \pm \sqrt{\left (\frac{\sigma_{x} - \sigma_{y}}{2}\right)^2 + \tau_{xy}^2}\,\! \)

Maximum and minimum shear stresses

The maximum shear stress or maximum principal shear stress is equal to one-half the difference between the largest and smallest principal stresses, and acts on the plane that bisects the angle between the directions of the largest and smallest principal stresses, i.e. the plane of the maximum shear stress is oriented 45^\circ from the principal stress planes. The maximum shear stress is expressed as

\( \tau_\mathrm{max}=\frac{1}{2}\left|\sigma_\mathrm{max}-\sigma_\mathrm{min}\right|\,\! \)

Assuming \( \sigma_1\ge\sigma_2\ge\sigma_3\,\! \) then

\( \tau_\mathrm{max}=\frac{1}{2}\left|\sigma_1-\sigma_3\right|\,\! \)

The normal stress component acting on the plane for the maximum shear stress is non-zero and it is equal to

\( \sigma_\mathrm{n}=\frac{1}{2}\left(\sigma_1+\sigma_3\right)\,\! \)

Derivation of the maximum and minimum shear stresses[3][4][16][17][18][19][20]

Stress deviator tensor

The stress tensor \( \sigma_{ij}\,\! \) can be expressed as the sum of two other stress tensors:

a mean hydrostatic stress tensor or volumetric stress tensor or mean normal stress tensor, \( p\delta_{ij}\,\!, \) which tends to change the volume of the stressed body; and
a deviatoric component called the stress deviator tensor, \( s_{ij}\,\!, \) which tends to distort it.

So:

\( \sigma_{ij}= s_{ij} + p\delta_{ij},\, \)

where p\,\! is the mean stress given by

\( p=\frac{\sigma_{kk}}{3}=\frac{\sigma_{11}+\sigma_{22}+\sigma_{33}}{3}=\tfrac{1}{3}I_1.\, \)

Note that convention in solid mechanics differs slightly from what is listed above. In solid mechanics, pressure is generally defined as negative one-third the trace of the stress tensor.

The deviatoric stress tensor can be obtained by subtracting the hydrostatic stress tensor from the stress tensor:

\( \begin{align} \ s_{ij} &= \sigma_{ij} - \frac{\sigma_{kk}}{3}\delta_{ij},\,\\ \left[{\begin{matrix} s_{11} & s_{12} & s_{13} \\ s_{21} & s_{22} & s_{23} \\ s_{31} & s_{32} & s_{33} \\ \end{matrix}}\right] &=\left[{\begin{matrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \\ \end{matrix}}\right]-\left[{\begin{matrix} p & 0 & 0 \\ 0 & p & 0 \\ 0 & 0 & p \\ \end{matrix}}\right] \\ &=\left[{\begin{matrix} \sigma_{11}-p & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22}-p & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33}-p \\ \end{matrix}}\right]. \\ \end{align} \)

Invariants of the stress deviator tensor

As it is a second order tensor, the stress deviator tensor also has a set of invariants, which can be obtained using the same procedure used to calculate the invariants of the stress tensor. It can be shown that the principal directions of the stress deviator tensor \( s_{ij}\,\! \) are the same as the principal directions of the stress tensor \( \sigma_{ij}\,\!. \) Thus, the characteristic equation is

\( \left| s_{ij}- \lambda\delta_{ij} \right| = \lambda^3-J_1\lambda^2-J_2\lambda-J_3=0,\, \)

where \( J_1\,\!, J_2\,\! \) and \( J_3\,\! \) are the first, second, and third deviatoric stress invariants, respectively. Their values are the same (invariant) regardless of the orientation of the coordinate system chosen. These deviatoric stress invariants can be expressed as a function of the components of \( s_{ij}\,\! \) or its principal values \( s_1\,\!, s_2\,\!, and s_3\,\!, \) or alternatively, as a function of \( \sigma_{ij}\,\! \) or its principal values \( \sigma_1\,\!, \sigma_2\,\!, \) and \( \sigma_3\,\! \) . Thus,

\( \begin{align} J_1 &= s_{kk}=0,\, \\ J_2 &= \textstyle{\frac{1}{2}}s_{ij}s_{ji} \\ &= -s_1s_2 - s_2s_3 - s_3s_1 \\ &= \tfrac{1}{6}\left[(\sigma_{11} - \sigma_{22})^2 + (\sigma_{22} - \sigma_{33})^2 + (\sigma_{33} - \sigma_{11})^2 \right ] + \sigma_{12}^2 + \sigma_{23}^2 + \sigma_{31}^2 \\ &= \tfrac{1}{6}\left[(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2 \right ] \\ &= \tfrac{1}{3}I_1^2-I_2,\,\\ J_3 &= \det(s_{ij}) \\ &= \tfrac{1}{3}s_{ij}s_{jk}s_{ki} \\ &= s_1s_2s_3 \\ &= \tfrac{2}{27}I_1^3 - \tfrac{1}{3}I_1 I_2 + I_3.\, \end{align} \)

Because \( s_{kk}=0\,\!, \) the stress deviator tensor is in a state of pure shear.

A quantity called the equivalent stress or von Mises stress is commonly used in solid mechanics. The equivalent stress is defined as

\( \sigma_\mathrm e = \sqrt{3~J_2} = \sqrt{\tfrac{1}{2}~\left[(\sigma_1-\sigma_2)^2 + (\sigma_2-\sigma_3)^2 + (\sigma_3-\sigma_1)^2 \right]} \,. \)

Octahedral stresses
Figure 6. Octahedral stress planes

Considering the principal directions as the coordinate axes, a plane whose normal vector makes equal angles with each of the principal axes (i.e. having direction cosines equal to \( |1/\sqrt{3}|\,\!) \) is called an octahedral plane. There are a total of eight octahedral planes (Figure 6). The normal and shear components of the stress tensor on these planes are called octahedral normal stress \( \sigma_\mathrm{oct}\,\! \) and octahedral shear stress \( \tau_\mathrm{oct}\,\!, \) respectively.

Knowing that the stress tensor of point O (Figure 6) in the principal axes is

\( \sigma_{ij}= \begin{bmatrix} \sigma_1 & 0 & 0\\ 0 & \sigma_2 & 0\\ 0 & 0 & \sigma_3 \end{bmatrix} \,\! \)

the stress vector on an octahedral plane is then given by:

\( \begin{align} \mathbf{T}_\mathrm{oct}^{(\mathbf{n})}&= \sigma_{ij}n_i\mathbf{e}_j \\ &=\sigma_1n_1\mathbf{e}_1+\sigma_2n_2\mathbf{e}_2+\sigma_3n_3\mathbf{e}_3\\ &=\tfrac{1}{\sqrt{3}}(\sigma_1\mathbf{e}_1+\sigma_2\mathbf{e}_2+\sigma_3\mathbf{e}_3) \end{align} \,\! \)

The normal component of the stress vector at point O associated with the octahedral plane is

\( \begin{align} \sigma_\mathrm{oct} &= T^{(n)}_in_i \\ &=\sigma_{ij}n_in_j \\ &=\sigma_1n_1n_1+\sigma_2n_2n_2+\sigma_3n_3n_3 \\ &=\tfrac{1}{3}(\sigma_1+\sigma_2+\sigma_3)=\tfrac{1}{3}I_1 \end{align} \,\! \)

which is the mean normal stress or hydrostatic stress. This value is the same in all eight octahedral planes. The shear stress on the octahedral plane is then

\( \begin{align} \tau_\mathrm{oct} &=\sqrt{T_i^{(n)}T_i^{(n)}-\sigma_\mathrm{n}^2} \\ &=\left[\tfrac{1}{3}(\sigma_1^2+\sigma_2^2+\sigma_3^2)-\tfrac{1}{9}(\sigma_1+\sigma_2+\sigma_3)^2\right]^{1/2} \\ &=\tfrac{1}{3}\left[(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2\right]^{1/2} = \tfrac{1}{3}\sqrt{2I_1^2-6I_2} = \sqrt{\tfrac{2}{3}J_2} \end{align} \,\! \)

Alternative measures of stress
Main article: Stress measures

Other useful stress measures include the first and second Piola–Kirchhoff stress tensors, the Biot stress tensor, and the Kirchhoff stress tensor.
Piola–Kirchhoff stress tensor

In the case of finite deformations, the Piola–Kirchhoff stress tensors express the stress relative to the reference configuration. This is in contrast to the Cauchy stress tensor which expresses the stress relative to the present configuration. For infinitesimal deformations or rotations, the Cauchy and Piola–Kirchhoff tensors are identical.

Whereas the Cauchy stress tensor, \( \boldsymbol{\sigma} \) relates stresses in the current configuration, the deformation gradient and strain tensors are described by relating the motion to the reference configuration; thus not all tensors describing the state of the material are in either the reference or current configuration. Describing the stress, strain and deformation either in the reference or current configuration would make it easier to define constitutive models (for example, the Cauchy Stress tensor is variant to a pure rotation, while the deformation strain tensor is invariant; thus creating problems in defining a constitutive model that relates a varying tensor, in terms of an invariant one during pure rotation; as by definition constitutive models have to be invariant to pure rotations). The 1st Piola–Kirchhoff stress tensor, \boldsymbol{P} is one possible solution to this problem. It defines a family of tensors, which describe the configuration of the body in either the current or the reference state.

The 1st Piola–Kirchhoff stress tensor, \( \boldsymbol{P} \) relates forces in the present configuration with areas in the reference ("material") configuration.

\( \boldsymbol{P} = J~\boldsymbol{\sigma}\cdot\boldsymbol{F}^{-T} \)

where \( \boldsymbol{F} \) is the deformation gradient and \( J= \det\boldsymbol{F} \) is the Jacobian determinant.

In terms of components with respect to an orthonormal basis, the first Piola–Kirchhoff stress is given by

\( P_{iL} = J~\sigma_{ik}~F^{-1}_{Lk} = J~\sigma_{ik}~\cfrac{\partial X_L}{\partial x_k}~\,\! \)

Because it relates different coordinate systems, the 1st Piola–Kirchhoff stress is a two-point tensor. In general, it is not symmetric. The 1st Piola–Kirchhoff stress is the 3D generalization of the 1D concept of engineering stress.

If the material rotates without a change in stress state (rigid rotation), the components of the 1st Piola–Kirchhoff stress tensor will vary with material orientation.

The 1st Piola–Kirchhoff stress is energy conjugate to the deformation gradient.
2nd Piola–Kirchhoff stress tensor

Whereas the 1st Piola–Kirchhoff stress relates forces in the current configuration to areas in the reference configuration, the 2nd Piola–Kirchhoff stress tensor \( \boldsymbol{S} \) relates forces in the reference configuration to areas in the reference configuration. The force in the reference configuration is obtained via a mapping that preserves the relative relationship between the force direction and the area normal in the current configuration.

\( \boldsymbol{S} = J~\boldsymbol{F}^{-1}\cdot\boldsymbol{\sigma}\cdot\boldsymbol{F}^{-T} ~. \)

In index notation with respect to an orthonormal basis,

\( S_{IL}=J~F^{-1}_{Ik}~F^{-1}_{Lm}~\sigma_{km} = J~\cfrac{\partial X_I}{\partial x_k}~\cfrac{\partial X_L}{\partial x_m}~\sigma_{km} \!\,\! \)

This tensor is symmetric.

If the material rotates without a change in stress state (rigid rotation), the components of the 2nd Piola–Kirchhoff stress tensor remain constant, irrespective of material orientation.

The 2nd Piola–Kirchhoff stress tensor is energy conjugate to the Green–Lagrange finite strain tensor.
See also

Bending
Kelvin probe force microscope
Residual stress
Shot peening
Strain
Strain tensor
Stress–energy tensor
Stress–strain curve
Stress concentration
Transient friction loading
Virial stress
Yield stress
Yield surface
Virial theorem

References

^ Walter D. Pilkey, Orrin H. Pilkey (1974). Mechanics of solids. p. 292.
^ a b c Mase
^ a b c d e Atanackovic
^ a b c d Chen & Han 2007
^ Smith & Truesdell 1993, p. 97
^ Slaughter
^ a b c Irgens
^ a b c Liu
^ a b Chadwick
^ Lubliner
^ Truesdell & Topin 1960
^ Fung
^ Basar
^ Hjelmstad
^ Hamrock
^ Wu
^ Chatterjee
^ Jaeger
^ Ameen 2005
^ Prager

Bibliography

Ameen, Mohammed (2005). Computational elasticity: theory of elasticity and finite and boundary element methods. Alpha Science Int'l Ltd.. pp. 33–66. ISBN 1-84265-201-X.
Atanackovic, Teodor M.; Guran, Ardéshir (2000). Theory of elasticity for scientists and engineers. Springer. pp. 1–46. ISBN 0-8176-4072-X.
Chadwick, Peter (1999). Continuum mechanics: concise theory and problems. Dover books on physics (2 ed.). Dover Publications. pp. 90–106. ISBN 0-486-40180-4.
Chakrabarty, J. (2006). Theory of plasticity (3 ed.). Butterworth-Heinemann. pp. 17–32. ISBN 0-7506-6638-2.
Chatterjee, Rabindranath (1999). Mathematical Theory of Continuum Mechanics. Alpha Science Int'l Ltd.. pp. 111–157. ISBN 81-7319-244-8.
Chen, Wai-Fah; Han, Da-Jian (2007). Plasticity for structural engineers. J. Ross Publishing. pp. 46–71. ISBN 1-932159-75-4.
Fung, Yuan-cheng; Tong, Pin (2001). Classical and computational solid mechanics. Volume 1 of Advanced series in engineering science. World Scientific. pp. 66–96. ISBN 981-02-4124-0.
Hamrock, Bernard (2005). Fundamentals of Machine Elements. McGraw-Hill. pp. 58–59. ISBN 0-07-297682-9.
Hjelmstad, Keith D. (2005). Fundamentals of structural mechanics. Prentice-Hall international series in civil engineering and engineering mechanics (2 ed.). Springer. pp. 103–130. ISBN 0-387-23330-X.
Irgens, Fridtjov (2008). Continuum mechanics. Springer. pp. 42–81. ISBN 3-540-74297-2.
Jaeger, John Conrad; Cook, N.G.W, & Zimmerman, R.W. (2007). Fundamentals of rock mechanics (Fourth ed.). Wiley-Blackwell. pp. 9–41. ISBN 0-632-05759-9.
Lubliner, Jacob (2008). Plasticity Theory (Revised Edition). Dover Publications. ISBN 0-486-46290-0.
Mase, George E. (1970). Continuum Mechanics. McGraw-Hill. pp. 44–76. ISBN 0-07-040663-4.
Mase, G. Thomas; George E. Mase (1999). Continuum Mechanics for Engineers (Second ed.). CRC Press. pp. 47–102. ISBN 0-8493-1855-6.
Prager, William (2004). Introduction to mechanics of continua. Dover Publications. pp. 43–61. ISBN 0-486-43809-0.
Smith, Donald Ray; Truesdell, Clifford (1993). An introduction to continuum mechanics -after Truesdell and Noll. Springer. ISBN 0-7923-2454-4.
Wu, Han-Chin (2005). Continuum mechanics and plasticity. CRC Press. pp. 45–78. ISBN 1-58488-363-4.

.

Stress (mechanics)