.

A distributed Bragg reflector (DBR) is a high quality reflector used in waveguides, such as optical fibers. It is a structure formed from multiple layers of alternating materials with varying refractive index, or by periodic variation of some characteristic (such as height) of a dielectric waveguide, resulting in periodic variation in the effective refractive index in the guide. Each layer boundary causes a partial reflection of an optical wave. For waves whose wavelength is close to four times the optical thickness of the layers, the many reflections combine with constructive interference, and the layers act as a high-quality reflector. The range of wavelengths that are reflected is called the photonic stopband. Within this range of wavelengths, light is "forbidden" to propagate in the structure.

Reflectivity

The reflectivity (R) of the DBR is given by

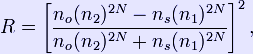
where and , are the respective refractive indices of the surrounding medium, the two alternating materials, and the substrate; and N is the number of repeated pairs of low/high refractive index material.

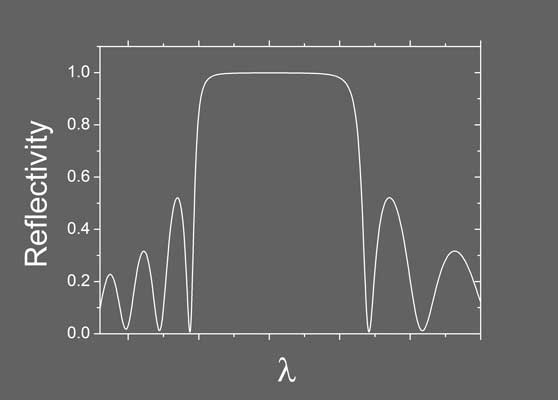
Calculated reflectivity of a schematic DBR structure

The bandwidth Δν₀ of the photonic stopband can be calculated by

where νo is the central frequency of the band.

Thus increasing the number of pairs in a DBR increases the mirror reflectivity and increasing the refractive index contrast between the materials in the Bragg pairs increases both the reflectivity and the bandwidth.

Distributed Bragg reflectors are critical components in vertical cavity surface emitting lasers and other types of narrow-linewidth laser diodes such as distributed feedback lasers. They are also used to form the cavity resonator (or optical cavity) in fiber lasers and free electron lasers.

TE and TM mode reflectivity

This section discusses the interaction of Transverse Electric and Transverse Magnetic polarized light with the DBR structure, over several wavelengths and incidence angles. This reflectivity of the DBR structure (described below) was calculated using the Transfer matrix method (TMM), where the TE mode alone gets highly reflected by this stack, while the TM modes are passed through. This also shows the DBR acting as a polarizer.

For TE and TM incidence we have the reflection spectra of a DBR stack, corresponding to a 6 layer stack of dielectric contrast of 11.5, between an air-dielectric layers. The thickness of air layer is 0.8 of the period, and dielectric is 0.2 of the period. The wavelength in the figures below, correspond in multiples of the cell-period.

This DBR also corresponds to a simple example of 1D Photonic Crystal's that have only a complete TE band gap, while only a pseudo TM band gap.

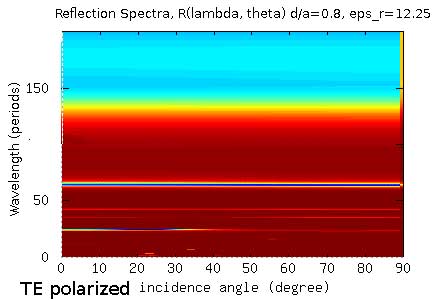
Calculated reflectivity for TE mode light at various incidence angles, and wavelengths. Red regions correspond to R=1, while blue regions correspond to R=0, and other colors 0 < R < 1. (*)

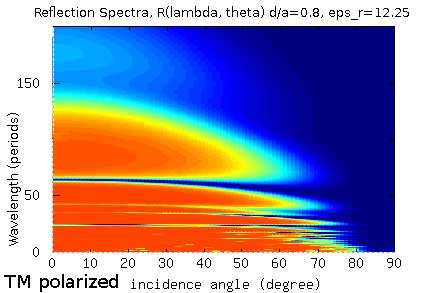
Calculated reflectivity for TM mode light at various incidence angles, and wavelengths. Orange regions correspond to R=1, while blue regions correspond to R=0, and other colors 0 < R < 1. (*)