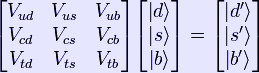Cabibbo-Kobayashi-Maskawa matrix

In the standard model of particle physics the Cabibbo-Kobayashi-Maskawa matrix (CKM matrix, quark mixing matrix, sometimes earlier called KM matrix) is a unitary matrix which contains information on the strength of flavour-changing weak decays. Technically, it specifies the mismatch of quantum states of quarks when they propagate freely and when they take part in the weak interactions. It is important in the understanding of CP violations. A precise mathematical definition of this matrix is given in the article on the formulation of the standard model. This matrix was introduced for three generations of quarks by Makoto Kobayashi and Toshihide Maskawa, adding one generation to the matrix previously introduced by Nicola Cabibbo.

The matrix

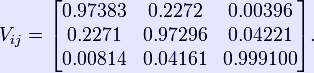
On the left is the CKM Matrix along with a vector of mass eigenstates of the quarks, and on the right is the weak force eigenstates of the quarks. The CKM matrix describes the probability of a transition from one quark q to another quark q' . This transition is proportional to .

Experimentally, combining a large number of independent measurements, the magnitudes of the values in the matrix have been found to be[1] (only central values presented here, uncertainties are excluded):

Counting

To proceed further, it is necessary to count the number of parameters in this matrix, V which appear in experiments, and therefore are physically important. If there are N generations of quarks (2N flavours) then

1. An N×N complex matrix contains 2N² real numbers.

2. The constraint of unitarity is ∑k V_ikV*_jk = δij. Therefore, for the diagonal terms (i=j) there are N constraints, and for the remaining terms, N(N−1). The number of independent real numbers in a unitary matrix is therefore N2.

3. One phase can be absorbed into each quark field. An overall common phase is unobservable. Hence there are 2N−1 fewer independent numbers, giving the total number of free variables to be (N−1)2.

4. Of these, N(N−1)/2 are rotation angles called quark mixing angles.

5. The remaining (N−1)(N−2)/2 are complex phases, which cause CP violation.

For the case N=2, there is only one parameter which is a mixing angle between two generations of quarks. Historically, this was the first version of CKM matrix when only two generations were known. It is called the Cabibbo angle after its inventor Nicola Cabibbo.

For the Standard Model case N=3, there are three mixing angles and one CP-violating complex phase.

Observations and predictions

Cabibbo's idea originated from a need to explain two observed phenomena:

1. the transitions u↔d and e↔ν_e, μ↔ν_μ had similar amplitudes.

2. the transitions with change in strangeness ΔS=1 had amplitudes equal to 1/4 of those with ΔS=0.

Cabibbo's solution consisted of postulating weak universality to resolve issue 1, along with a mixing angle θc, now called the Cabibbo angle, between the d and s quarks to resolve issue 2.

For two generations of quarks, there are no CP violating phases, as shown by the counting of the previous section. Since CP violations were seen in neutral kaon decays already in 1964, the emergence of the standard model soon after was a clear signal of the existence of a third generation of quarks, as pointed out in 1973 by Kobayashi and Maskawa. The discovery of the bottom quark at Fermilab (by Leon Lederman's group) in 1976 therefore immediately started off the search for the missing third-generation quark, the top quark.

Weak universality

The constraints of unitarity of the CKM-matrix on the diagonal terms can be written as

∑ | V_ik | 2 = 1
k

for all generations i. This implies that the sum of all couplings of any of the up-type quarks to all the down-type quarks is the same for all generations. This relation is called weak universality after Nicola Cabibbo, who first pointed it out in 1967. Theoretically it is a consequence of the fact that all SU(2) doublets couple with the same strength to the vector bosons of weak interactions. It has been subjected to continuing experimental tests.

The unitarity triangles

The remaining constraints of unitarity of the CKM-matrix can be written in the form

For any fixed and different i and j, this is a constraint on three complex numbers, one for each k, which says that these numbers form the sides of a triangle in the complex plane. There are six choices of i and j, and hence six such triangles, each of which is called an unitary triangle. Their shapes can be very different, but they all have the same area, which can be related to the CP violating phase. The area vanishes for the specific parameters in the standard model for which there would be no CP violation. The orientation of the triangles depend on the phases of the quark fields.

Since the three sides of the triangles are open to direct experiment, as are the three angles, a class of tests of the standard model is to check that the triangle closes. This is the purpose of a modern series of experiments under way at the Japanese BELLE and the Californian BaBar experiments.

See also

* Formulation of the standard model and CP violations.

* Quantum chromodynamics, flavour and strong CP problem.

* MNS matrix, the equivalent mixing matrix for neutrinos.

References

1. ^ W.-M. Yao et al., J. Phys. G 33, 1 (2006) and 2007 partial update for the 2008 edition available on the PDG WWW pages (URL: http://pdg.lbl.gov/), Chapter 11. The CKM Quark-Mixing Matrix

* Griffiths, David J. (1987). Introduction to Elementary Particles. Wiley, John & Sons, Inc. ISBN 0-471-60386-4.

* Povh, Bogdan et al., (1995). Particles and Nuclei: An Introduction to the Physical Concepts. New York: Springer. ISBN 3-540-20168-8

Links

* CP violation, by I.I. Bigi and A.I. Sanda (Cambridge University Press, 2000) [ISBN 0-521-44349-0]

* Particle Data Group: the CKM matrix

* Particle Data Group: CP violation in meson decays

* The Babar experiment at SLAC and the BELLE experiment at KEK Japan

* N. Cabibbo, Phys. Rev. Lett. 10 (1963) 531.

* M. Kobayashi and K. Maskawa, Prog. Theor. Phys. 49 (1973) 652.