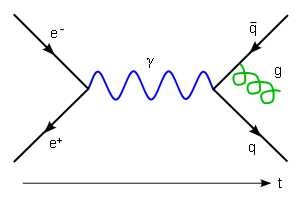
In this Feynman diagram, an electron and positron annihilate producing a virtual photon that becomes a quark-antiquark pair. Then one radiates a gluon. In the field of solid-state physics similar diagrams are also used, where typically the photon is replaced by a phonon.
Feynman diagrams are a pictorial representation of a term in a perturbative expansion of the scattering amplitude for the experiment defined by the incoming and outgoing lines. In some quantum field theories (notably quantum electrodynamics), one can obtain an excellent approximation of the scattering amplitude from a few terms of the perturbative expansion, corresponding to a few simple Feynman diagrams with the same incoming and outgoing lines connected by different vertices and internal lines.
The method, although originally invented for particle physics, has somewhat informally been adopted in solid-state physics, where the behavior of phonons may be expressed by analogy to that of photons, for example in the theory of superconductivity.
Feynman diagrams are frequently confused with spacetime diagrams and bubble chamber images because of their visual similarity, but the connection is weak. Feynman diagrams are merely graphs; there is no concept of position or space in a Feynman diagram, and there is no concept of time aside from the distinction between incoming and outgoing lines. Additionally, only a collection of Feynman diagrams can be said to represent any given particle interaction; particles do not choose a particular diagram each time they interact.
Motivation and history
The problem of calculating scattering cross sections in particle physics reduces to summing over the amplitudes of all possible intermediate states (each corresponding to one term in the perturbation expansion which is known as the Dyson series). These states can be represented by Feynman diagrams, which are much easier to keep track of than frequently tortuous calculations. Feynman showed how to calculate diagram amplitudes using so-called Feynman rules, which can be derived from the system's underlying Lagrangian. Each internal line corresponds to a factor of the corresponding virtual particle's propagator; each vertex where lines meet gives a factor derived from an interaction term in the Lagrangian, and incoming and outgoing lines provide constraints on energy, momentum, and spin. A Feynman diagram is therefore a symbolic notation for the factors appearing in each term of the Dyson series.
However, being a perturbative expansion, nonperturbative effects do not show up in Feynman diagrams.
In addition to their value as a mathematical tool, Feynman diagrams provide deep physical insight to the nature of particle interactions. Particles interact in every way available; in fact, intermediate virtual particles are allowed to propagate faster than light. The probability of each final state is then obtained by summing over all such possibilities. This is closely tied to the functional integral formulation of quantum mechanics, also invented by Feynman–see path integral formulation.
The naïve application of such calculations often produces diagrams whose amplitudes are infinite, which is undesirable in a physical theory. The problem is that particle self-interactions are erroneously ignored. The technique of renormalization, pioneered by Feynman, Schwinger, and Tomonaga compensates for this effect and eliminates the troublesome infinite terms. After such renormalization, calculations using Feynman diagrams often match experimental results with very good accuracy.
Feynman diagram and path integral methods are also used in statistical mechanics.
Penguin diagrams
John Ellis was the first to refer to a certain class of Feynman diagrams as penguin diagrams, due in part to their shape, and in part to a legendary bar-room bet with Melissa Franklin. According to John Ellis:[1]
“
Mary K. [Gaillard], Dimitri [Nanopoulos] and I first got interested in what are now called penguin diagrams while we were studying CP violation in the Standard Model in 1976... The penguin name came in 1977, as follows.
In the spring of 1977, Mike Chanowitz, Mary K and I wrote a paper on GUTs predicting the b quark mass before it was found. When it was found a few weeks later, Mary K, Dimitri, Serge Rudaz and I immediately started working on its phenomenology. That summer, there was a student at CERN, Melissa Franklin who is now an experimentalist at Harvard. One evening, she, I and Serge went to a pub, and she and I started a game of darts. We made a bet that if I lost I had to put the word penguin into my next paper. She actually left the darts game before the end, and was replaced by Serge, who beat me. Nevertheless, I felt obligated to carry out the conditions of the bet.
For some time, it was not clear to me how to get the word into this b quark paper that we were writing at the time. Then, one evening, after working at CERN, I stopped on my way back to my apartment to visit some friends living in Meyrin where I smoked some illegal substance. Later, when I got back to my apartment and continued working on our paper, I had a sudden flash that the famous diagrams look like penguins. So we put the name into our paper, and the rest, as they say, is history.
”Thorsten Ohl's paper on generating Feynman diagrams with LaTeX (see the external links) illustrates their penguin-like shape.
In 1991 and 1994, the CLEO collaboration provided the first experimental evidence for these processes.
Alternative names
Murray Gell-Mann always referred to Feynman diagrams as Stückelberg diagrams, after a Swiss physicist, Ernst Stückelberg, who devised a similar notation.[2]
Historically they were also called Feynman-Dyson diagrams or Dyson graphs[3].
Interpretation
Feynman diagrams are really a graphical way of keeping track of deWitt indices, much like Penrose's graphical notation for indices in multilinear algebra. There are several different types for the indices, one for each field (this depends on how the fields are grouped; for instance, if the up quark field and down quark field are treated as different fields, then there would be different type assigned to both of them but if they are treated as a single multicomponent field with "flavors", then there would only be one type). The edges, (i.e., propagators) are tensors of rank (2,0) in deWitt's notation (i.e., with two contravariant indices and no covariant indices), while the vertices of degree n are rank n covariant tensors which are totally symmetric among all bosonic indices of the same type and totally antisymmetric among all fermionic indices of the same type and the contraction of a propagator with a rank n covariant tensor is indicated by an edge incident to a vertex (there is no ambiguity in which "slot" to contract with because the vertices correspond to totally symmetric tensors). The external vertices correspond to the uncontracted contravariant indices.
A derivation of the Feynman rules using Gaussian functional integrals is given in the functional integral article.
Each Feynman diagram on its own does not have a physical significance. It's only the infinite sum over all possible (bubble-free) Feynman diagrams which gives physical results. Unfortunately, this infinite sum is only asymptotically convergent.
Mathematical details
Main article: Feynman graph
A Feynman diagram can be considered as a graph. When considering a field composed of particles, the edges will represent (sections of) particle world lines; the vertices represent virtual interactions. Since only certain interactions are permitted, the graph is constrained to have only certain types of vertices. The type of field of an edge is its field label; the permitted types of interaction are interaction labels.
The value of a given diagram can be derived from the graph; the value of the interaction as a whole is obtained by summing over all diagrams.
See also
* Stückelberg-Feynman interpretation
* Invariance mechanics
References
- ^ [hep-ph/9510397] ITEP Lectures in Particle Physics
- ^ The Jaguar and the Fox - 00.07
- '^ Gribbin, John and Mary. Richard Feynman: A Life in Science, Penguin-Putnam, 1997 Ch 5.
- Gerardus 't Hooft, Martinus Veltman, Diagrammar, CERN Yellow Report 1973, online
- David Kaiser, Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics, Chicago: University of Chicago Press, 2005. ISBN 0-226-42266-6
- Martinus Veltman, Diagrammatica: The Path to Feynman Diagrams, Cambridge Lecture Notes in Physics, ISBN 0-521-45692-4 (expanded, updated version of above)
 Feynman Diagrams
Feynman Diagrams
Links