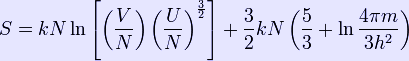| - Art Gallery - |
The Joule expansion is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container (via a small partition), with the other side of the container being evacuated; the partition between the two parts of the container is then opened, and the gas fills the whole container. This process is a useful exercise in classical thermodynamics, as it is easy to work out the resulting increase in entropy. One mole of ideal gas (at pressure Pi and temperature Ti) is confined to the left-hand side (as drawn) of a thermally isolated container, and occupies a volume V0. The right hand side of the container, also containing a volume V0, is evacuated. The tap (solid line) between the two halves of the container is then suddenly opened and the gas fills the entire container, of volume 2V0. We propose that both the previous and new temperature and pressure (Tf, Pf) follow the Ideal Gas Law, so that initially we have PiVi = RTi and then, when the tap is opened, we have PfVf = RTf, where R is the ideal gas constant. As the system is thermally isolated, the change in internal energy ΔU = 0, and because the internal energy is a function of temperature only for the ideal gas, we know that ΔT = 0 also, and so Ti = Tf. This implies that PiV0 = Pf(2V0), and thus the pressure halves; i.e. Pf= Pi/2. Entropy changes It is awkward to calculate the change in entropy in this process directly, because the route that the expansion takes in the time between the partition being opened and the equilibrium state being reached involves states that are far from thermal equilibrium and would require specifying the complete velocity distribution of the molecules to be defined. However, entropy is a function of state, and therefore the entropy change can be computed directly from the knowledge of the final and initial equilibrium states. For an ideal monatomic gas, the entropy as a function of the internal energy, volume and number of particles is given by the Sackur–Tetrode equation: It is seen that a doubling of the volume at constant internal energy will lead to an entropy increase of: ΔS = Nkln(2) = nRln(2) This result is also valid if the gas is not monatomic, as the volume dependence of an ideal gas in the dilute limit (in which classical statistical mechanics correctly describes the translational degrees of freedom) is the same as for a monatomic gas. One can also evaluate the entropy change using purely thermodynamic methods. It is necessary to then take another route from the initial state to the final state, such that all the intermediary states are in thermal equilibrium. This means that such a route can only be realized in the limit where the changes happen infinitely slowly. Such routes are also referred to as quasistatic routes. In some books one demands that a quasistatic route has to be reversible, here we don't add this extra condition. The net entropy change from the initial state to the final state is independent of the particular choice of the quasistatic route, as the entropy is a function of state. Suppose that instead of letting the gas undergo a free expansion in which the volume is doubled, a free expansion in allowed which the volume expands by a very small amount dV. After thermal equilibrium is reached, we then let the gas undergo another free expansion by dV and wait until thermal equilibrium is reached. We repeat this until the volume has been doubled. In the limit dV to zero, this becomes an ideal quasistatic process, albeit an irreversible one. Now, according to the fundamental thermodynamic relation, we have: dU = TdS − PdV As this equation relates changes in thermodynamic state variables, it is valid for any quasistatic change, regardless of whether it is irreversible or reversible. For the above defined path we have that dU = 0 and thus T\,dS=P\,dV, and hence the change in entropy for the Joule expansion is Another path that can be chosen is to let the system undergo a reversible adiabatic expansion in which the volume is doubled. The system will then perform work, so we'll have to supply energy to the system equal to the work performed to make sure it ends up in the same final state as in case of Joule expansion. During the reversible adiabatic expansion, we have dS = 0, hence dU = − PdV. For an ideal gas we also have dU = CvdT. The temperature after the doubling of the volume is thus given as: Heating the gas up to the initial temperature of T0 quasistatically will increase the entropy by:
We have calculated ΔSgas above; we can proceed to infer ΔSsurroundings and ΔSuniverse as follows: the system is thermally isolated, so the surroundings cannot exchange heat with the gas, and therefore ΔSsurroundings = 0 . Hence ΔSuniverse = ΔSsurroundings + ΔSgas = Rln2. We might ask what the entropy would be if, once the Joule expansion has occurred, the gas is put back into the left-hand side by compressing it. The best method (i.e. the method involving the least work) is that of a reversible isothermal compression, which would take work ΔW (for one mole) given by References The majority of good undergraduate textbooks deal with this expansion in great depth; see e.g. Concepts in Thermal Physics, Blundell & Blundell, OUP ISBN 0-19-856770-7
Retrieved from "http://en.wikipedia.org/"  |
|