Αριθμός e (μαθηματικά)

O αριθμός e (στα ελληνικά λέγεται έψιλον ή απλά "ε") είναι ένας άρρητος αριθμός και ταυτόχρονα η βάση των φυσικών ή νεπέριων λογαρίθμων. Συχνά καλείται και αριθμός του Όυλερ (Euler) ή σταθερά του Ναπιέρ. Eίναι ένας από τους σημαντικότερους αριθμούς στα μαθηματικά. Υπάρχει μια ποικιλία ισοδύναμων ορισμών του αριθμού e. Η αξία του, με προσέγγιση τριακοστού δεκαδικού ψηφίου είναι:

e ≈ 2.71828 18284 59045 23536 02874 71352

Ορισμοί

Με όριο

Ο e είναι το όριο της ακολουθίας

Εδώ αξίζει να σημειώσουμε ότι ο παραπάνω όρος εμφανίζεται στο πρόβλημα του ανατοκισμού. Συγκεκριμένα είναι το ποσό που θα εισπράξει κάποιος ο οποίος καταθέτει σήμερα μία νομισματική μονάδα μετά από n περιόδους με n περιόδους τοκισμού σε κάθε περίοδο. Αν πάρουμε την οριακή περίπτωση ο αριθμός των περιόδων να τείνει στο άπειρο τότε θα εισπράξουμε e νομισματικές μονάδες και όχι άπειρα χρήματα που ίσως θα περιμέναμε! Το πρόβλημα σε αυτή τη διάσταση μελέτησε ο Jacob Bernoulli ο οποίος έδειξε ότι το ανάπτυγμα σε απειροσειρά του συγκλίνει σε ένα αριθμό στο διάστημα (2,3)

Με το άθροισμα μιας άπειρης σειράς

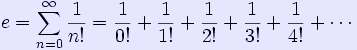
Με εμβαδό υπερβολής f(t) = 1 / t

Από τον αριθμό στη Συνάρτηση

Αν και πέρασαν πολλά χρόνια μέχρι να οριστεί η εκθετική συνάρτηση, από την στιγμή του ορισμού της έγινε μία από τις διασημότερες (αν όχι η διασημότερη) συνάρτηση. Η συνάρτηση έχει την εξαιρετική ιδιότητα να ισούται με την παράγωγο της. Αυτό σημαίνει περιγράφει μεγέθη που πολλαπλασιάζονται με σταθερό ρυθμό (ή σταθερή ένταση) κάτι το οποίο συναντάμε σε πάρα πολλές εφαρμογές ως το πρώτο βήμα για να δομήσουμε πιο πολύπλοκα μοντέλα.

Η συνάρτηση f(x) = e^x προσεγγίζεται μέσω του αναπτύγματος της σειράς

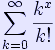
Μια σχέση φανταστική!

O Όυλερ κατελήξε στην παρακάτω σχέση για έναν φανταστικό αριθμό

Για να δείξει το παραπάνω αποτέλεσμα ο Όυλερ έκανε κάποια λάθη στον χειρισμό των σειρών που ανέπτυξε αλλά το αποτέλεσμα παραμένει.

Αν θέσουμε παίρνουμε

Η τελευταία σχέση είναι γνωστή ως εξίσωση του Όυλερ και είναι μία από τις σημαντικότερες στην φιλοσοφία των Μαθηματικών. Συνδέει τους \,e,\pi,i με την μονάδα και το μηδέν, χρησιμοποιώντας πρόσθεση, πολλαπλασιασμό και ύψωση σε δύναμη! Πέρα από την φιλοσοφία, η σχέση αυτή μας έδωσε και κάτι παραπάνω. Χρησιμοποιήθηκε στην απόδειξη ότι ο π είναι υπερβατικός, δηλαδή ότι δεν αποτελεί λύση κάποιας πολυωνυμικής εξίσωσης. Τέτοιος αριθμός είναι και ο e.

Πρόταση: Για n διαφορετικούς αλγεβρικούς αριθμούς a₁,a₂,..,a_n και επίσης αλγεβρικούς αριθμούς A₁,A₂,..,A_n όχι όλους ίσους με το μηδέν η παράσταση

δεν ισούται με το μηδέν.(Λιντερμαν)

Η εξίσωση του Όυλερ όμως μας δίνει ένα τέτοιο αποτέλεσμα για τον αριθμό iπ άρα και για τον π. Συνεπώς ο π είναι υπερβατικός. Αυτό έδωσε τέλος στις προσπάθειες τετραγωνισμού του κύκλου, αφού αποδεικνύει ότι είναι αδύνατος.

Πηγές

* e: Η Ιστορία ενός Αριθμού, Eli Maor, Εκδόσεις Κάτοπτρο

.Ταυτότητα του Όιλερ