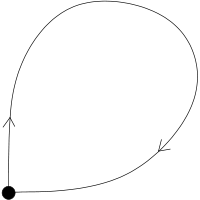
In mathematics, a homoclinic orbit is a trajectory of a flow of a dynamical system which joins a saddle equilibrium point to itself. More precisely, a homoclinic orbit lies in the intersection of the stable manifold and the unstable manifold of an equilibrium. Homoclinic orbits and homoclinic points are defined in the same way for iterated functions, as the intersection of the stable set and unstable set of some fixed point or periodic point of the system. Consider the continuous dynamical system described by the ODE
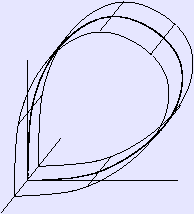
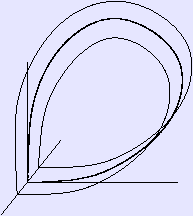
Suppose there is an equilibrium at x = x0, then a solution Φ(t) is a homoclinic orbit if If the phase space has three or more dimensions, then it is important to consider the topology of the unstable manifold of the saddle point. The figures show two cases. First, when the unstable manifold is topologically a cylinder, and secondly, when the unstable manifold is topologically a Möbius strip; in this case the homoclinic orbit is called twisted. We also have the notion of homoclinic orbit when considering discrete dynamical systems. In such a case, if
See also * Heteroclinic orbit
* John Guckenheimer and Philip Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Applied Mathematical Sciences Vol. 42), Springer
* Homoclinic orbits in Henon map with Java applets and comments Retrieved from "http://en.wikipedia.org/"
 |
|
is a diffeomorphism of a manifold M, we say that x is a homoclinic point if it has the same past and future - more specifically, if it exists a fixed (or periodic) point p such that
