The Mandelbrot set is a set of points in the complex plane, the boundary of which forms a fractal. Mathematically, the Mandelbrot set can be defined as the set of complex c-values for which the orbit of 0 under iteration of the complex quadratic polynomial xn+1=xn2 + c remains bounded.[1] Eg. c = 1 gives the sequence 0, 1, 2, 5, 26… which tends to infinity. As this sequence is unbounded, 1 is not an element of the Mandelbrot set. On the other hand, c = i gives the sequence 0, i, (-1 + i), –i, (-1 + i), -i… which is bounded, and so it belongs to the Mandelbrot set. When computed and graphed on the complex plane, the Mandelbrot Set is seen to have an elaborate boundary, which does not simplify at any given magnification. This qualifies the boundary as a fractal. The Mandelbrot set has become popular outside mathematics both for its aesthetic appeal and for being a complicated structure arising from a simple definition. Benoît Mandelbrot and others worked hard to communicate this area of mathematics to the public. History The Mandelbrot set has its place in complex dynamics, a field first investigated by the French mathematicians Pierre Fatou and Gaston Julia at the beginning of the 20th century. The first pictures of it were drawn in 1978 by Robert Brooks and Peter Matelski as part of a study of Kleinian Groups.[2] Mandelbrot studied the parameter space of quadratic polynomials in an article that appeared in 1980.[3] The mathematical study of the Mandelbrot set really began with work by the mathematicians Adrien Douady and John H. Hubbard[4], who established many fundamental properties of M and named the set in honour of Mandelbrot. The mathematicians Heinz-Otto Peitgen and Peter Richter became well-known for promoting the set with glossy photographs, books, and a touring gallery.[5] The cover article of the August 1985 Scientific American featured an image created by Mandelbrot, Peitgen, and Hubbard. [6] The work of Douady and Hubbard coincided with a huge increase in interest in complex dynamics and abstract mathematics, and the study of the Mandelbrot set has been a centerpiece of this field ever since. An exhaustive list of all the mathematicians who have contributed to the understanding of this set since then is beyond the scope of this article, but such a list would notably include Mikhail Lyubich,[7] [8], Curt McMullen, John Milnor, Mitsuhiro Shishikura, and Jean-Christophe Yoccoz. Formal definition The Mandelbrot set M is defined by a family of complex quadratic polynomials given by where c is a complex parameter. For each c, one considers the behavior of the sequence More formally, if Mathematically, the Mandelbrot set is just a set of complex numbers. A given complex number c either belongs to M or it does not. A picture of the Mandelbrot set can be made by colouring all the points c which belong to M black, and all other points white. The more colourful pictures usually seen are generated by colouring points not in the set according to how quickly or slowly the sequence The Mandelbrot set can also be defined as the connectedness locus of the family of polynomials Pc(z). That is, it is the subset of the complex plane consisting of those parameters c for which the Julia set of Pc is connected. Basic properties The Mandelbrot set is a compact set, contained in the closed disk of radius 2 around the origin. In fact, a point c belongs to the Mandelbrot set if and only if The intersection of M with the real axis is precisely the interval The correspondence is given by
In fact, this gives a correspondence between the entire parameter space of the logistic family and that of the Mandelbrot set. The area of the Mandelbrot set is estimated to be 1.506 591 77 ± 0.000 000 08. Douady and Hubbard have shown that the Mandelbrot set is connected. In fact, they constructed an explicit conformal isomorphism between the complement of the Mandelbrot set and the complement of the closed unit disk. Mandelbrot had originally conjectured that the Mandelbrot set is disconnected. This conjecture was based on computer pictures generated by programs which are unable to detect the thin filaments connecting different parts of M. Upon further experiments, he revised his conjecture, deciding that M should be connected. The dynamical formula for the uniformisation of the complement of the Mandelbrot set, arising from Douady and Hubbard's proof of the connectedness of M, gives rise to external rays of the Mandelbrot set. These rays can be used to study the Mandelbrot set in combinatorial terms and form the backbone of the Yoccoz parapuzzle. The boundary of the Mandelbrot set is exactly the bifurcation locus of the quadratic family; that is, the set of parameters c for which the dynamics changes abruptly under small changes of c. It can be constructed as the limit set of a sequence of plane algebraic curves, the Mandelbrot curves, of the general type known as polynomial lemniscates. The Mandelbrot curves are defined by setting p0=z, pn=pn-12+z, and then interpreting the set of points |pn(z)|=1 in the complex plane as a curve in the real Cartesian plane of degree 2n+1 in x and y.
Other properties Upon looking at a picture of the Mandelbrot set, one immediately notices the large cardioid-shaped region in the center. This main cardioid is the region of parameters c for which Pc has an attracting fixed point. It consists of all parameters of the form for some \mu\, in the open unit disk. To the left of the main cardioid, attached to it at the point c = − 3 / 4, a circular-shaped bulb is visible. This bulb consists of those parameters c , for which Pc has an attracting cycle of period 2. This set of parameters is an actual circle, namely that of radius 1/4 around -1. There are infinitely many other bulbs tangent to the main cardioid: for every rational number This bulb is called the he change of behavior occurring at Hyperbolic components All the bulbs we encountered in the previous section were interior components of the Mandelbrot set in which the maps It is conjectured that these are the only interior regions of M. This problem, known as density of hyperbolicity, may be the most important open problem in the field of complex dynamics. Hypothetical non-hyperbolic components of the Mandelbrot set are often referred to as "queer" components. For real quadratic polynomials, this question was answered positively in the 1990s independently by Lyubich and by Graczyk and Świątek. (Note that hyperbolic components intersecting the real axis correspond exactly to periodic windows in the Feigenbaum diagram. So this result states that such windows exist near every parameter in the diagram.) Not every hyperbolic component can be reached by a sequence of direct bifurcations from the main cardioid of the Mandelbrot set. However, such a component can be reached by a sequence of direct bifurcations from the main cardioid of a little Mandelbrot copy (see below). Local connectivity It is conjectured that the Mandelbrot set is locally connected. This famous conjecture is known as MLC (for Mandelbrot Locally Connected). By the work of Adrien Douady and John H. Hubbard, this conjecture would result in a simple abstract "pinched disk" model of the Mandelbrot set. In particular, it would imply the important hyperbolicity conjecture mentioned above. The celebrated work of Jean-Christophe Yoccoz established local connectivity of the Mandelbrot set at all finitely-renormalizable parameters; that is, roughly speaking those which are contained only in finitely many small Mandelbrot copies. Since then, local connectivity has been proved at many other points of M, but the full conjecture is still open. Self-similarity The Mandelbrot set is self-similar under magnification in the neighborhoods of the Misiurewicz points. It is also conjectured to be self-similar around generalized Feigenbaum points (e.g. -1.401155 or -.1528 + 1.0397i), in the sense of converging to a limit set.[9][10] The Mandelbrot set in general is not strictly self-similar but it is quasi-self-similar, as small slightly different versions of itself can be found at arbitrarily small scales. The little copies of the Mandelbrot set are all slightly different, mostly because of the thin threads connecting them to the main body of the set. Further results The Hausdorff dimension of the boundary of the Mandelbrot set equals 2 as determined by a result of Mitsuhiro Shishikura.[11] It is not known whether the boundary of the Mandelbrot set has positive planar Lebesgue measure. In the Blum-Shub-Smale model of real computation, the Mandelbrot set is not computable, but its complement is computably enumerable. However, many simple objects (e.g., the graph of exponentiation) are also not computable in the BSS model. At present it is unknown whether the Mandelbrot set is computable in models of real computation based on computable analysis, which correspond more closely to the intuitive notion of "plotting the set by a computer." Hertling has shown that the Mandelbrot set is computable in this model if the hyperbolicity conjecture is true. Relationship with Julia sets As a consequence of the definition of the Mandelbrot set, there is a close correspondence between the geometry of the Mandelbrot set at a given point and the structure of the corresponding Julia set. This principle is exploited in virtually all deep results on the Mandelbrot set. For example, Shishikura proves that, for a dense set of parameters in the boundary of the Mandelbrot set, the Julia set has Hausdorff dimension two, and then transfers this information to the parameter plane. Similarly, Yoccoz first proves the local connectivity of Julia sets, before establishing it for the Mandelbrot set at the corresponding parameters. Adrien Douady phrases this principle as Plough in the dynamical plane, and harvest in parameter space. Geometry Recall that, for every rational number A period q-limb will have q − 1 "antennae" at the top of its limb. We can thus determine the period of a given bulb by counting these antennas. Mandelbrot set drawings algorithms References 1. ^ Mandelbrot Set Explorer: Mathematical Glossary. Retrieved on 2007-10-07. 2. ^ Robert Brooks and Peter Matelski, The dynamics of 2-generator subgroups of PSL(2,C), in "Riemann Surfaces and Related Topics", ed. Kra and Maskit, Ann. Math. Stud. 97, 65–71, ISBN 0-691-08264-2 3. ^ Benoît Mandelbrot, Fractal aspects of the iteration of z\mapsto\lambda z(1-z)\, for complex \lambda,z\,, Annals NY Acad. Sci. 357, 249/259 4. ^ Adrien Douady and John H. Hubbard, Etude dynamique des polynômes complexes, Prépublications mathémathiques d'Orsay 2/4 (1984 / 1985) 5. ^ Chaos: Making a New Science. James Gleick. 1987. p 229. 6. ^ Fractals: The Patterns of Chaos. John Briggs. 1992. p 80. 7. ^ Lyubich, Mikhail (May-June, 1999). "Six Lectures on Real and Complex Dynamics". Retrieved on 2007-04-04. 8. ^ Lyubich, Mikhail (November 1998). "Regular and stochastic dynamics in the real quadratic family". Proceedings of the National Academy of Sciences of the United States of America 95: 14025-14027. doi:10.1073/pnas.95.24.14025. Retrieved on 2007-04-04. 9. ^ T. Lei, "Similarity between the Mandelbrot set and Julia Sets", Communications in Mathematical Physics 134 (1990), pp. 587-617. 10. ^ J. Milnor, "Self-Similarity and Hairiness in the Mandelbrot Set", in Computers in Geometry and Topology, M. Tangora (editor), Dekker, New York, pp. 211-257. 11. ^ Mitsuhiro Shishikura, The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets, Ann. of Math. 147 (1998) p. 225-267. (First appeared in 1991 as a Stony Brook IMS Preprint, available as arXiv:math.DS/9201282.) 12. ^ http://www.iec.csic.es/~miguel/Preprint3.ps | M. Romera, G. Pastor, and F. Montoya Drawing the Mandelbrot set by the method of the escape lines In Fractalia 5, No. 17, 11-13 (1996) 13. ^ García, Francisco; Ángel Fernández, Javier Barrallo, Luis Martín. "Coloring Dynamical Systems in the Complex Plane" (PDF). Retrieved on 2008-01-21. Further reading * Lennart Carleson and Theodore W. Gamelin, Complex Dynamics, Springer 1993, ISBN 0-387-97942-5 * John W. Milnor, Dynamics in One Complex Variable (Third Edition), Annals of Mathematics Studies 160, Princeton University Press 2006, ISBN 0-691-12488-4 (First appeared in 1990 as a Stony Brook IMS Preprint, available as arXiV:math.DS/9201272.) * Nigel Lesmoir-Gordon. "The Colours of Infinity: The Beauty, The Power and the Sense of Fractals." ISBN 1-904555-05-5 (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set. Links * Chaos and Fractals at the Open Directory Project * The Mandelbrot Set and Julia Sets by Michael Frame, Benoit Mandelbrot, and Nial Neger Retrieved from "http://en.wikipedia.org/" |
|
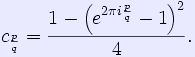obtained by iterating Pc(z) starting at critical point 
,, which either escapes to infinity or stays within a disk of some finite radius. The Mandelbrot set is defined as the set of all points c such that the above sequence does not escape to infinity.
denotes the nth iterate of Pc(z) (i.e. Pc(z) composed with itself n times), the Mandelbrot set is the subset of the complex plane given by
diverges to infinity. See the section on computer drawings below for more details.
for all 
. In other words, if the absolute value of 
ever becomes larger than 2, the sequence will escape to infinity.
,. The parameters along this interval can be put in one-to-one correspondence with those of the real logistic family,
,
.
, with p and q coprime, there is such a bulb that is tangent at the parameter
. 
-fixed point). If we label these components 
in counterclockwise orientation, then Pc maps the component Uj to the component 
.
is known as a bifurcation: the attracting fixed point "collides" with a repelling period q-cycle. As we pass through the bifurcation parameter into the 
, have an attracting periodic cycle. Such components are called hyperbolic components.