In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle.

More specifically, consider a triangle ABC, and a point P that is not one of the vertices A, B, C. Drop perpendiculars from P to the three sides of the triangle (these may need to be produced, i.e., extended). Label L, M, N the intersections of the lines from P with the sides BC, AC, AB. The pedal triangle is then LMN.

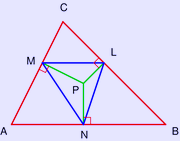
A triangle in red, the perpendiculars from a point P in green, and the obtained pedal triangle in blue.

The location of the chosen point P relative to the chosen triangle ABC gives rise to some special cases:

* If P = orthocenter, then LMN = orthic triangle.

* If P = incenter, then LMN = intouch triangle.

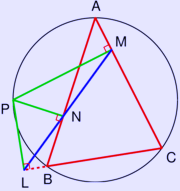
The case when P is on the circumcircle, and the pedal triangle degenerates into a line (blue).

If P is on the circumcircle of the triangle, LMN collapses to a line. This is then called the pedal line, or sometimes the Simson line after Robert Simson.

If P has trilinear coordinates p : q : r, then the vertices L,M,N of the pedal triangle of P are given by

* L = 0 : q + p cos C : r + p cos B

* M = p + q cos A : 0 : r + q cos A

* N = p + r cos B : q + r cos B : 0

The A-vertex, L', of the antipedal triangle of P is the point of intersection of the perpendicular to BP through B and the perpendicular to CP through C. The B-vertex, M ', and the C-vertex, N ', are constucted analogously. Trilinear coordinates are given by

* L' = - (q + p cos C)(r + p cos B) : (r + p cos B)(p + q cos C) : (q + p cos C)(p + r cos B)

* M' = (r + q cos A)(q + p cos C) : - (r + q cos A)(p + q cos C) : (p + q cos C)(q + r cos A)

* N' = (q + r cos A)(r + p cos B) : (p + r cos B)(r + q cos A) : - (p + r cos B)(q + r cos A)

For example, the excentral triangle is the antipedal triangle of the incenter.

Suppose that P does not lie on a sideline, BC, CA, AB, and let P - 1 denote the isogonal conjugate of P. The pedal triangle of P is homothetic to the antipedal triangle of P - 1. The homothetic center (which is a triangle center if and only if P is a triangle center) is the point given in trilinear coordinates by

ap(p + q cos C)(p + r cos B) : bq(q + r cos A)(q + p cos C) : cr(r + p cos B)(r + q cos A).

Another theorem about the pedal triangle of P and the antipedal triangle of P - 1 is that the product of their areas equals the square of the area of triangle ABC.

See also

* Simson line

Links

* Mathworld: Pedal Triangle

* Java Applet of the Perpendiculars

* Pedal Triangle and Isogonal Conjugacy

Geometry