.

In geometry, given a triangle and a point on its circumcircle, the intersections formed when lines are constructed from the point perpendicular to each of the triangle's sides are collinear. The line through these points is the Simson line, named for Robert Simson.

The converse is also true; if the feet of the perpendiculars dropped from a point to the sides of the triangle are collinear, then the point is on the circumcircle. The Simson line of a point is just the pedal triangle of it; the case when that pedal triangle degenerates to a line.

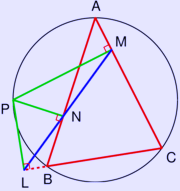
The Simson line LNM of the triangle ABC.

Properties

* The Simson line of a vertex of the triangle is the altitude of the triangle dropped from that vertex, and the Simson line of the point diametrically opposite to the vertex is the side of the triangle opposite to that vertex.

* If P and P' are points on the circumcircle, then the angle between the Simson lines of P and P' is half the angle of the arc PP'. In particular, if the points are diametrically opposite, their Simson lines are perpendicular and in this case the intersection of the lines is on the nine-point circle.

* Let H denote the orthocenter of the triangle ABC, then the Simson line of P bisects the segment PH in a point that lies on the nine-point circle.

* Given two triangles with the same circumcircle, the angle between the Simson lines of a point P on the circumcircle for both triangles doesn't depend of P.

Proof of existence

The method of proof is to show that . PBCA is a cyclic quadrilateral, so . PNMA is a cyclic quadrilateral (Thales' theorem), so . Hence . Now PLBN is cyclic, so . Therefore .