- Eric W. Weisstein, Pentagon at MathWorld.
- How to construct a regular pentagon using only compass and straightedge
- Definition and properties of the pentagon, with interactive animation
- Nine constructions for the regular pentagon by Robin Hu
- Renaissance artists' approximate constructions of regular pentagons at Convergence
.
Pentagon
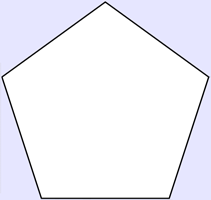
A regular pentagon, {5}
| Regular pentagon | |
|---|---|
| Edges and vertices | 5 |
| Schläfli symbol | {5} |
| Coxeter–Dynkin diagram | 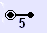 |
| Symmetry group | Dihedral (D5) |
| Area (with t=edge length) |
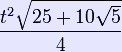 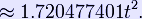 |
| Internal angle (degrees) |
108° |
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The internal angles in a simple pentagon total 540°.
Regular pentagons
The term pentagon is commonly used to mean a regular convex pentagon, where all sides are equal and all interior angles are equal (to 108°). Its Schläfli symbol is {5}.
The area of a regular convex pentagon with side length t is given by 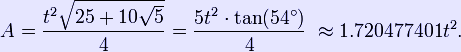
A pentagram is a regular star pentagon. Its Schläfli symbol is {5/2}. Its sides form the diagonals of a regular convex pentagon - in this arrangement the sides of the two pentagons are in the golden ratio.
Construction
A regular pentagon is constructible using a compass and straightedge, either by inscribing one in a given circle or constructing one on a given edge. This process was described by Euclid in his Elements circa 300 BC.
One method to construct a regular pentagon in a given circle is as follows:

Construction of a regular pentagon
1. Draw a circle in which to inscribe the pentagon and mark the center point O. (This is the green circle in the diagram to the right).
2. Choose a point A on the circle that will serve as one vertex of the pentagon. Draw a line through O and A.
3. Construct a line perpendicular to the line OA passing through O. Mark its intersection with one side of the circle as the point B.
4. Construct the point C as the midpoint of O and B.
5. Draw a circle centered at C through the point A. Mark its intersection with the line OB (inside the original circle) as the point D.
6. Draw a circle centered at A through the point D. Mark its intersections with the original (green) circle as the points E and F.
7. Draw a circle centered at E through the point A. Mark its other intersection with the original circle as the point G.
8. Draw a circle centered at F through the point A. Mark its other intersection with the original circle as the point H.
9. Construct the regular pentagon AEGHF.
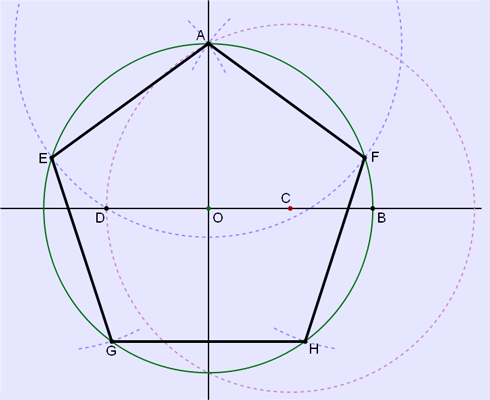
Constructing a pentagon
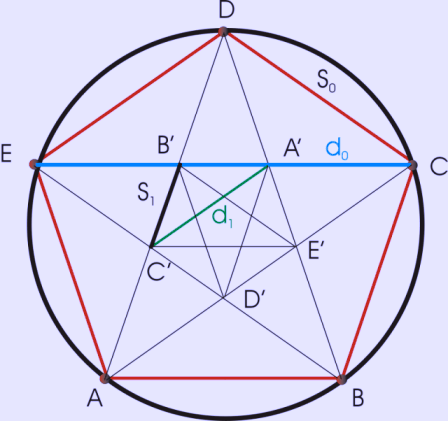
After forming a regular convex pentagon, if you join the non-adjacent corners (drawing the diagonals of the pentagon), you obtain a pentagram, with a smaller regular pentagon in the center. Or if you extend the sides until the non-adjacent ones meet, you obtain a larger pentagram.
Links
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License