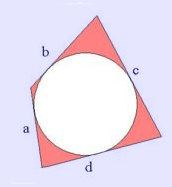
Tangential quadrilateral. The circle does not have to be inscribed as shown in order for it to be tangential In geometry, a tangential quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle. Because tangential quadrilaterals can be drawn surrounding or circumscribing their incircles, they are also sometimes called circumscribed quadrilaterals or circumscribable quadrilaterals. Another name for the same class of quadrilaterals is inscriptable quadrilaterals. Example Examples of tangential quadrilaterals are squares, rhombi, and kites. If a quadrilateral is both tangential and cyclic, it is called bicentric. Characterization In a tangential quadrilateral, the four angle bisectors meet at the center of the inscribed circle, and conversely a convex quadrilateral in which the four angle bisectors meet at a point must be tangential. In a tangential quadrilateral, the two pairs of opposite sides add to the same total length, which equals the semiperimeter of the quadrilateral:
Conversely a convex quadrilateral in which a + c = b + d must be tangential. Wu Wei Chao (2000) observed another characterization of tangential quadrilaterals. The two diagonals of any convex quadrilateral partition the quadrilateral into four triangles. Let r1, r2, r3, and r4 denote the radii of the circles inscribed in each of these triangles; then the quadrilateral is tangential if and only if
Area The area of a tangential quadrilateral is
where s is the semiperimeter described above and r is the circle's radius (called the inradius). References * Chao, Wu Wei; Simeonov, Plamen (2000). "When quadrilaterals have inscribed circles (solution to problem 10698)". American Mathematical Monthly 107 (7): 657–658. * Eric W. Weisstein, Tangential Quadrilateral at MathWorld. Retrieved from "http://en.wikipedia.org/" |
|