Quadrilateral

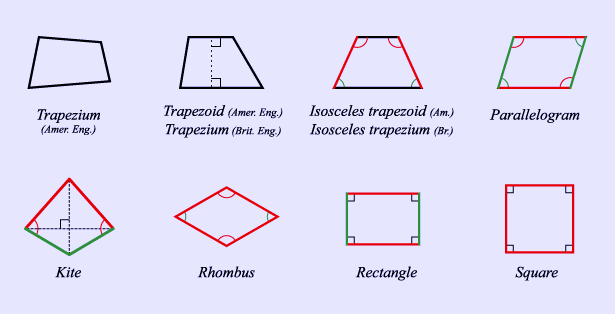
In geometry, a quadrilateral is a polygon with four sides or edges and four vertices or corners. Sometimes, the term quadrangle is used, for etymological symmetry with triangle, and sometimes tetragon for consistency with pentagon (5 sided), hexagon (6 sided) and so on. However, the term quadrangle could be considered incorrect, as the laws of Euclid state that an angle's degree measure must be less than 180, and so a concave quadrilateral has only 3 angles.[citation needed] The interior angles of a quadrilateral add up to 360 degrees.

Quadrilaterals are either simple (not self-intersecting) or complex (self-intersecting). Simple quadrilaterals are either convex or concave.

Convex quadrilaterals

Convex quadrilaterals are further classified as follows:

* Trapezium (British English) or trapezoid (Amer.): two opposite sides are parallel.

* Isosceles trapezium (Brit.) or isosceles trapezoid (Amer.): two opposite sides are parallel, the two other sides are of equal length, and the two ends of each parallel side have equal angles. This implies that the diagonals are of equal length.

* Trapezium (Amer.): no sides are parallel.

* Parallelogram: both pairs of opposite sides are parallel. This implies that opposite sides are of equal length, opposite angles are equal, and the diagonals bisect each other.

* Kite: two adjacent sides are of equal length and the other two sides also of equal length. This implies that one set of opposite angles is equal, and that one diagonal perpendicularly bisects the other. (It is common, especially in the discussions on plane tessellations, to refer to a concave kite as a dart or arrowhead.)

* Rhombus or rhomb: all four sides are of equal length. This implies that opposite sides are parallel, opposite angles are equal, and the diagonals perpendicularly bisect each other.

* Rhomboid: a parallelogram in which adjacent sides are of unequal lengths and angles are oblique (not right angles).

* Rectangle (or Oblong): all four angles are right angles. This implies that opposite sides are parallel and of equal length, and the diagonals bisect each other and are equal in length.

* Square (regular quadrilateral): all four sides are of equal length (equilateral), and all four angles are equal (equiangular), with each angle a right angle. This implies that opposite sides are parallel (a square is a parallelogram), and that the diagonals perpendicularly bisect each other and are of equal length. A quadrilateral is a square if and only if it is both a rhombus and a rectangle.

* Cyclic quadrilateral: the four vertices lie on a circumscribed circle.

* Tangential quadrilateral: the four edges are tangential to an inscribed circle. Another term for a tangential polygon is inscriptible.

* Bicentric quadrilateral: both cyclic and tangential.

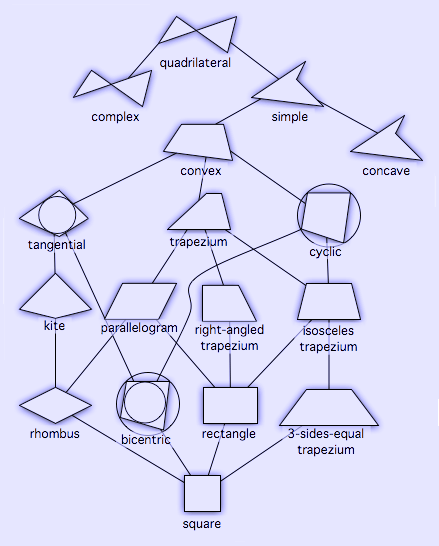
More quadrilaterals

* An geometric chevron [arrowhead] has bilateral symmetry like a kite, but the top concaves inwards.

* A self-intersecting quadrilateral is called variously a cross-quadrilateral, butterfly quadrilateral or bow-tie quadrilateral.

* An equiangular quadrilateral is a rectangle if convex, and an "angular eight" with corners on a rectangle if non-convex.

* In solid geometry, a quadrilateral whose vertices do not all lie in a flat plane is a skew quadrilateral. Opposite sides in a skew quadrilateral are (segments of) skew lines.

Taxonomy

A taxonomy of quadrilaterals is illustrated by the following graph. Lower forms are special cases of higher forms. Note that "trapezium" here is referring to the British definition (the American equivalent is a trapezoid).

Links

* Eric W. Weisstein, Quadrilateral at MathWorld.

* Van Aubel's theorem and Varignon and Wittenbauer Parallelograms by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"

* Compendium Geometry Analytic Geometry of Quadrilaterals

* Quadrilaterals Formed by Perpendicular Bisectors, Projective Collinearity and Interactive Classification of Quadrilaterals from cut-the-knot

* Definitions and examples of quadrilaterals and Definition and properties of tetragons from Mathopenref

Geometry