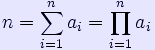An amenable number is an integer for which there exists a multiset of as many integers as the original number that can be either added up or multiplied together to give the original number. To put it algebraically, for an integer n, there is a multiset of n integers {a1, ... , an}, for which the equalities

hold. Negative numbers are allowed in the multiset. For example, 5 is amenable since 5 = 1 + (-1) + 1 + (-1) + 5. All numbers congruent to 0 or 1, mod 4, except 4, are amenable.

All composite numbers would be amenable if the multiset was allowed to be of any length, because, even if other solutions are available, one can always make an inelegant solution by taking the prime factorization (expressed with repeated factors rather than exponents) and add as many 1s as necessary to add up to n. Because of the multiplicative identity, multiplying this set of integers will yield n no matter how many 1s there are in the set.

To allow any prime number to be amenable, negative numbers are usually required. Even if no other solutions are available, one can always make an inelegant solution for a prime number p of {1, -1, 1, -1, p}. In the sum, the positive ones are cancelled out by the negative ones, leaving p, while in the product, the two negative ones cancel out the effect of their signs, leaving only the multiplicative identity to affect the final result.

Amenable numbers should not be confused with amicable numbers, which are pairs of integers whose divisors add up to each other.

References

* Mathworld article

* Sloane's A100832

* Lossers, O. P. "Solution to Problem 10454. Amenable Numbers." American Mathematical Monthly 105, 1998.

* Tamvakis, H. "Problem 10454." American Mathematical Monthly 102, 463, 1995.

Number Theory