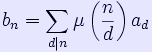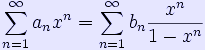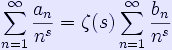Möbius transform

In mathematics, the Möbius transform Tf of a function f defined on the positive integers is defined by

where μ is the classic Möbius function. In more common usage, the function Tf is called the Möbius inverse of f.

(The notation d | n means d is a divisor of n.)

This function is named in honor of August Ferdinand Möbius.

The transform takes multiplicative functions to multiplicative functions. On Dirichlet series generating functions it corresponds to division by the Riemann zeta function.

Series relations

Let

so that

be its transform. The transforms are related by means of series: the Lambert series

and the Dirichlet series:

where ζ(s) is the Riemann zeta function.

See also

* Möbius inversion formula

Number Theory