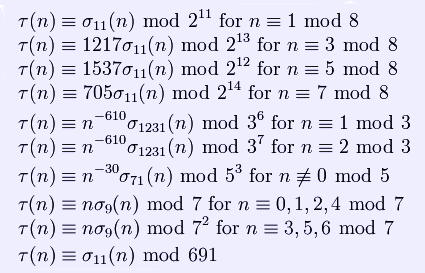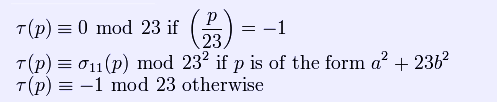Ramanujan's tau function

The Ramanujan tau function is the function defined by the following identity:

The first few values of the tau function are given in the following table (sequence A000594 in OEIS):

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
τ(n)	1	−24	252	−1472	4830	−6048	−16744	84480	−113643	−115920	534612	−370944	−577738	401856	1217160	987136

If one substitutes q = exp(2πiz) with then the function defined by

is a holomorphic cusp form of weight 12 and level 1, known as the discriminant modular form.

Ramanujan observed, but could not prove, the following three properties of τ(n):

* τ(mn) = τ(m)τ(n) if gcd(m,n) = 1 (meaning that τ(n) is a multiplicative function)

* τ(p^{r + 1}) = τ(p)τ(p_^r) − p¹¹τ(p^{r − 1}) for p prime and

* for all primes p

The first two properties were proved by Mordell in 1917 and the third one was proved by Deligne in 1974.

Congruences for the tau function

For } and , define σ_k(n) as the sum of the k-th powers of the divisors of n. The tau functions satisfies several congruence relations; many of them can be expressed in terms of σ_k(n). Here are some:

For prime, we have

Number Theory