In four dimensional geometry, the bitruncated 5-cell, or bitruncated pentachoron, is a 4-dimensional polytope, or polychoron, composed of 10 cells in the shape of truncated tetrahedra. Each hexagonal face of the truncated tetrahedra is joined in complementary orientation to the neighboring truncated tetrahedron. Each edge is shared by two hexagons and one triangle. Each vertex is surrounded by 4 truncated tetrahedral cells in a tetragonal disphenoid vertex figure.

The bitruncated 5-cell is the intersection of two pentachora in dual configuration. As such, it is also the intersection of a penteract with the hyperplane that bisects the penteract's long diagonal orthogonally. In this sense it is the 4-dimensional analog of the regular octahedron (intersection of regular tetrahedra in dual configuration / tesseract bisection on long diagonal) and the regular hexagon (equilateral triangles / cube). The 5-dimensional analog is the birectified hexateron, and the n-dimensional analog is the polytope whose Coxeter–Dynkin diagram is linear with rings on the middle one or two nodes.

The bitruncated 5-cell is one of the two non-regular uniform polychora which are cell-transitive. The other is the bitruncated 24-cell, which is composed of 48 truncated cubes.
Alternative names

* Bitruncated pentachoron
* Bitruncated pentatope
* Bitruncated 4-simplex
* (Truncated-tetrahedral) decachoron
* Deca (Jonathan Bowers: for decachoron)

Coordinates

The Cartesian coordinates of an origin-centered bitruncated 5-cell having edge length 2 are:

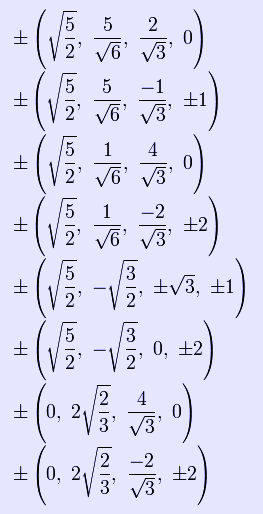
These vertices can be more simply constructed on a hyperplane in 5-space as the permutations of:

(0,0,1,2,2)

Related uniform polychora

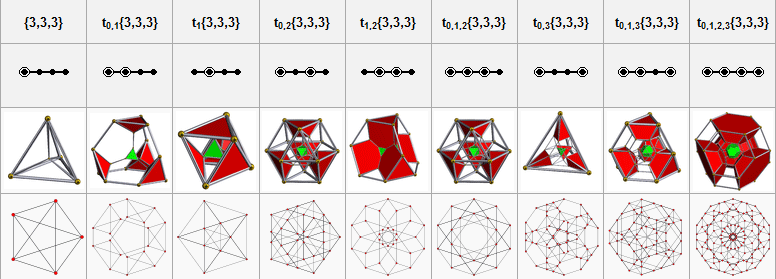
The bitruncated pentachoron is one of 9 uniform polychora constructed from the [3,3,3] Coxeter group.

Name	5-cell	truncated 5-cell	rectified 5-cell	cantellated 5-cell	bitruncated 5-cell	cantitruncated 5-cell	runcinated 5-cell	runcitruncated 5-cell	omnitruncated 5-cell
Schläfli symbol
Coxeter-Dynkin diagram
Schlegel diagram
Coxeter plane projection

Images: Robert Webb's Great Stella software