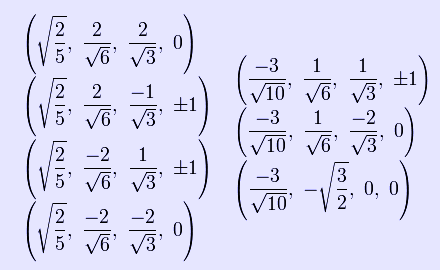Rectified 5-cell

In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.

It is one of three semiregular polychora made of two or more cells which are platonic solids, discovered by Thorold Gosset in his 1900 paper. He called it a Tetroctahedric for being made of tetrahedron and octahedron cells.

The vertex figure of the rectified 5-cell is a uniform triangular prism, formed by three octahedra around the sides, and two tetrahedra on the opposite ends.

Alternate names

* Dispentachoron
* Rectified 5-cell (Norman W. Johnson)
* Rectified pentachoron
* Rectified 4-simplex
* Rap (Jonathan Bowers: for rectified pentachoron)
* Ambopentachoron (Neil Sloane & John Horton Conway)

Images

Coordinates

The Cartesian coordinates of the vertices of an origin-centered rectified 5-cell having edge length 2 are:

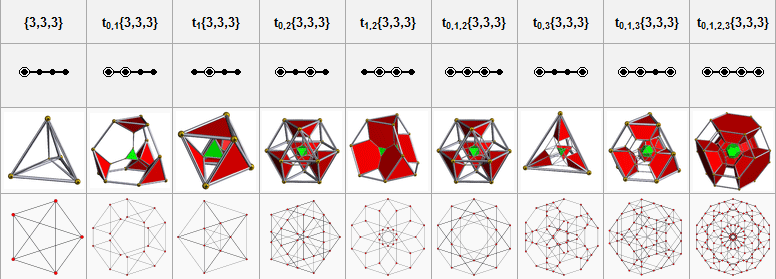
These vertices can be more simply constructed on a hyperplane in 5-space as the permutations of:

(0,0,0,1,1)

This construction is from the positive orthant facet of the rectified pentacross.

Related uniform polychora

The rectified pentachoron is one of 9 uniform polychora constructed from the [3,3,3] Coxeter group.

Name	5-cell	truncated 5-cell	rectified 5-cell	cantellated 5-cell	bitruncated 5-cell	cantitruncated 5-cell	runcinated 5-cell	runcitruncated 5-cell	omnitruncated 5-cell
Schläfli symbol
Coxeter-Dynkin diagram
Schlegel diagram
Coxeter plane projection

Images: Robert Webb's Great Stella software

Geometry