In four dimensional geometry, the omnitruncated 5-cell is a uniform polychoron. It is composed of 120 vertices, 240 edges, 150 faces (90 squares and 60 hexagons), and 30 cells. The cells are: 10 truncated octahedra, and 20 hexagonal prisms. Each vertex is surrounded by four cells: two truncated octahedra, and two hexagonal prisms, arranged in two chiral irregular tetrahedral vertex figures. Coxeter calls this Hinton's polytope after C. H. Hinton, who described it in his book The Fourth Dimension in 1906. It forms a uniform honeycomb which Coxeter calls Hinton's honeycomb.[1] * Omnitruncated 5-cell
Orthogonal projection in A4 Coxeter plane Schlegel diagram centered on truncated octahedron Permutohedron Just as the truncated octahedron is the permutohedron of order 4, the omnitruncated 5-cell is the permutohedron of order 5.[2] The omnitruncated 5-cell is a zonotope, the Minkowski sum of five line segments parallel to the five lines through the origin and the five vertices of the 5-cell. Tessellations The omnitruncated 5-cell can tessellate 4-dimensional space by translational copies, each with 3 hypercells around each face. It has Coxeter-Dynkin diagram of CD downbranch-11.pngCD downbranch-33.pngCD righttriangleopen 111.png.[3] Unlike the 3d honeycomb analogy, the bitruncated cubic honeycomb, which has three different Coxeter group Wythoff constructions, this honeycomb has only one such construction.[1] Coordinates The Cartesian coordinates of the vertices of an origin-centered omnitruncated 5-cell having edge length 2 are: These vertices can be more simply obtained in 5-space as the 120 permutations of (0,1,2,3,4). This construction is from the positive orthant facet of the omnitruncated pentacross. Related uniform polychora The omnitruncated pentachoron is one of 9 uniform polychora constructed from the [3,3,3] Coxeter group.
Images: Robert Webb's Great Stella software Retrieved from "http://en.wikipedia.org/" |
|
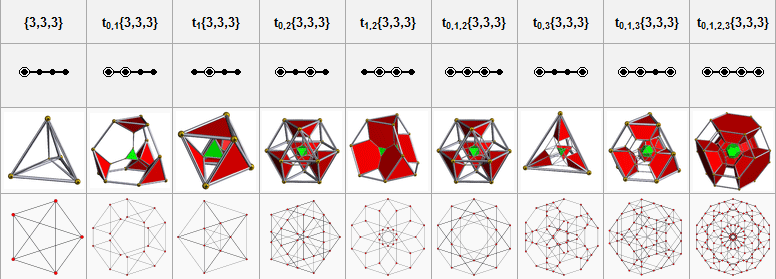
||||||||||||||||||||||||||